题目内容
15.(1)若(x-1)x+2=1,则x的值为-2,0,2.(2)若(x-1)x+1=1,则x的值为-1,2.
(3)若${(x+2)}^{{x}^{2}-4}$=1,则x的值为-1,2.
分析 (1)分3种情况讨论:当指数为0,底数不等于0时,求出x的值;当底数为-1,指数为偶数时求出x的值;当底数为1,时求出x的值;
(2)分3种情况讨论:当指数为0,底数不等于0时,求出x的值;当底数为-1,指数为偶数时求出x的值;当底数为1,时求出x的值;
(3)分3种情况讨论:当指数为0,底数不等于0时,求出x的值;当底数为-1,指数为偶数时求出x的值;当底数为1,时求出x的值.
解答 解:(1)当x+2=0时,x=-2,
原式=(-3)0=1,符合题意,
则x=-2;
当x-1=-1时,x=0,
原式=(-1)2=1,符合题意,
则x=0;
当x-1=1时,x=2,
原式=(1)4=1,符合题意,
则x=2;
(2)当x+1=0时,x=-1,
原式=(-2)0=1,符合题意,
则x=-1;
当x-1=-1时,x=0,
原式=(-1)1=-1,不符合题意;
当x-1=1时,x=2,
原式=(1)3=1,符合题意,
则x=2;
(3)${(x+2)}^{{x}^{2}-4}$=1,
当x2-4=0时,x=±2,
x=2时,原式=40=1,符合题意,
x=-2时,底数为0,不符合题意,
则x=2;
当x+2=-1时,x=-3,
原式=(-1)5=-1,不符合题意;
当x+2=1时,x=-1,
原式=(1)-3=1,符合题意,
则x=-1;
故答案为:-2,0,2;-1,2;-1,2.
点评 本题考查了零指数幂和有理数的乘方,解答本题的关键是分情况进行讨论求出各种情况下的x的值,注意不要漏解.

练习册系列答案
相关题目
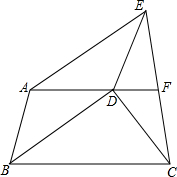 A、D、F在同一直线上,F是CE的中点,EC⊥BC、BA∥DE,BD∥AE.甲、乙两人同时从住所B地步行到F地办公,若甲走的路线是B-A-E-F;乙走的路线是B-D-C-F,假设两人行走的速度相同,那么谁先到达办公地点F?请说明理由.
A、D、F在同一直线上,F是CE的中点,EC⊥BC、BA∥DE,BD∥AE.甲、乙两人同时从住所B地步行到F地办公,若甲走的路线是B-A-E-F;乙走的路线是B-D-C-F,假设两人行走的速度相同,那么谁先到达办公地点F?请说明理由.