题目内容
5.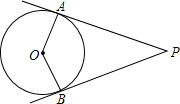 如图,点P在⊙O外,PA,PB分别与⊙O相切于A,B两点,∠P=50°,则∠AOB等于130°.
如图,点P在⊙O外,PA,PB分别与⊙O相切于A,B两点,∠P=50°,则∠AOB等于130°.
分析 由PA与PB为圆的两条切线,利用切线性质得到PA与OA垂直,PB与OB垂直,在四边形APBO中,利用四边形的内角和定理即可求出∠AOB的度数.
解答 解:∵PA、PB是⊙O的切线,
∴PA⊥OA,PB⊥OB,
∴∠PAO=∠PBO=90°,
∵∠P=50°,
∴∠AOB=130°.
故答案为:130°.
点评 此题考查了切线的性质,以及四边形的内角和定理,熟练掌握切线的性质是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.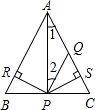 如图,已知在△ABC中,PR⊥AB于R,PS⊥AC于S,PR=PS,∠1=∠2,则四个结论:①AR=AS;②PQ∥AB;③△BPR≌△CPS;④BP=CP中( )
如图,已知在△ABC中,PR⊥AB于R,PS⊥AC于S,PR=PS,∠1=∠2,则四个结论:①AR=AS;②PQ∥AB;③△BPR≌△CPS;④BP=CP中( )
 如图,已知在△ABC中,PR⊥AB于R,PS⊥AC于S,PR=PS,∠1=∠2,则四个结论:①AR=AS;②PQ∥AB;③△BPR≌△CPS;④BP=CP中( )
如图,已知在△ABC中,PR⊥AB于R,PS⊥AC于S,PR=PS,∠1=∠2,则四个结论:①AR=AS;②PQ∥AB;③△BPR≌△CPS;④BP=CP中( )| A. | 全部正确 | B. | 仅①②正确 | C. | 仅①正确 | D. | 仅①④正确 |
13.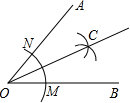 如图,用直尺和圆规作∠AOB的平分线的示意图如图所示,则下列选项中,能说明图中所作出的射线OC是∠AOB的平分线的依据是( )
如图,用直尺和圆规作∠AOB的平分线的示意图如图所示,则下列选项中,能说明图中所作出的射线OC是∠AOB的平分线的依据是( )
 如图,用直尺和圆规作∠AOB的平分线的示意图如图所示,则下列选项中,能说明图中所作出的射线OC是∠AOB的平分线的依据是( )
如图,用直尺和圆规作∠AOB的平分线的示意图如图所示,则下列选项中,能说明图中所作出的射线OC是∠AOB的平分线的依据是( )| A. | SSS | |
| B. | ASA | |
| C. | AAS | |
| D. | 角平分线是哪个的点到这个角两边的距离相等 |
14.数轴上到原点O距离3个单位长度的点表示的数是( )
| A. | -3 | B. | 3 | C. | -3或3 | D. | -3或0 |
 如图,已知△ABC中,∠ABC=45°,F是高AD和BE的交点,CD=3,则线段DF的长度为3.
如图,已知△ABC中,∠ABC=45°,F是高AD和BE的交点,CD=3,则线段DF的长度为3. 如图,已知△ABC中,AB=6,AC=9,AD⊥BC于D,M为AD上任一点,则MC2-MB2=45.
如图,已知△ABC中,AB=6,AC=9,AD⊥BC于D,M为AD上任一点,则MC2-MB2=45.