题目内容
10. 如图,在平面直角坐标系中,∠AOB=30°,点A的坐标为(2,0),过点A作AA1⊥OB,垂足为点A1,过A1作A1A2⊥x轴,垂足为点A2;再过点A2作A2A3⊥OB,垂足为点A3;再过点A3作A3A4⊥x轴,垂足为点A4…;这样一直作下去,则A2017的横坐标为( )
如图,在平面直角坐标系中,∠AOB=30°,点A的坐标为(2,0),过点A作AA1⊥OB,垂足为点A1,过A1作A1A2⊥x轴,垂足为点A2;再过点A2作A2A3⊥OB,垂足为点A3;再过点A3作A3A4⊥x轴,垂足为点A4…;这样一直作下去,则A2017的横坐标为( )| A. | $\frac{3}{2}$•($\frac{\sqrt{3}}{2}$)2015 | B. | $\frac{3}{2}$•($\frac{\sqrt{3}}{2}$)2016 | C. | $\frac{3}{2}$•($\frac{\sqrt{3}}{2}$)2017 | D. | $\frac{3}{2}$•($\frac{\sqrt{3}}{2}$)2018 |
分析 根据含30°的直角三角形的性质结合图形即可得到规律“OAn=($\frac{\sqrt{3}}{2}$)nOA=2($\frac{\sqrt{3}}{2}$)n,依此规律即可解决问题.
解答 解:∵∠AOB=30°,点A坐标为(2,0),
∴OA=2,
∴OA1=$\frac{\sqrt{3}}{2}$OA=$\sqrt{3}$,OA2=$\frac{\sqrt{3}}{2}$OA1═$\frac{3}{2}$,OA3=$\frac{\sqrt{3}}{2}$OA2═$\frac{3\sqrt{3}}{4}$,OA4=$\frac{\sqrt{3}}{2}$OA3═$\frac{9}{8}$,…,
∴OAn=($\frac{\sqrt{3}}{2}$)nOA=2($\frac{\sqrt{3}}{2}$)n.
∴OA2018=2×($\frac{\sqrt{3}}{2}$)2018=$\frac{3}{2}$•($\frac{\sqrt{3}}{2}$)2016
故选B.
点评 本题考查了规律型中点的坐标以及含30度角的直角三角形,利用“在直角三角形中,30°角所对的直角边等于斜边的一半”结合图形找出变化规律OAn=($\frac{\sqrt{3}}{2}$)nOA=2($\frac{\sqrt{3}}{2}$)n是解题的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
19. 在平面直角坐标系中,若干个半径为2个单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,沿这条曲线向右上下起伏运动,点在直线上的速度为2个单位长度/秒,点在弧线上的速度为$\frac{2π}{3}$个单位长度/秒,则2017秒时,点P的坐标是( )
在平面直角坐标系中,若干个半径为2个单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,沿这条曲线向右上下起伏运动,点在直线上的速度为2个单位长度/秒,点在弧线上的速度为$\frac{2π}{3}$个单位长度/秒,则2017秒时,点P的坐标是( )
 在平面直角坐标系中,若干个半径为2个单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,沿这条曲线向右上下起伏运动,点在直线上的速度为2个单位长度/秒,点在弧线上的速度为$\frac{2π}{3}$个单位长度/秒,则2017秒时,点P的坐标是( )
在平面直角坐标系中,若干个半径为2个单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,沿这条曲线向右上下起伏运动,点在直线上的速度为2个单位长度/秒,点在弧线上的速度为$\frac{2π}{3}$个单位长度/秒,则2017秒时,点P的坐标是( )| A. | (2017,0) | B. | (2017,$\sqrt{3}$) | C. | (2017,-$\sqrt{3}$) | D. | (2016,0) |
 某生物兴趣小组在四天的实验研究中发现:骆驼的体温会随外部环境温度的变化而变化,而且在这四天中每昼夜的体温变化情况相同,他们将一头骆驼前两昼夜的体温变化情况绘制成右图,请根据图象回答:
某生物兴趣小组在四天的实验研究中发现:骆驼的体温会随外部环境温度的变化而变化,而且在这四天中每昼夜的体温变化情况相同,他们将一头骆驼前两昼夜的体温变化情况绘制成右图,请根据图象回答: 如图,△ABC内接于⊙O,直径AB=8,D为BA延长线上一点且AD=4,E为线段CD上一点,满足∠EAC=∠BAC,则AE=2.
如图,△ABC内接于⊙O,直径AB=8,D为BA延长线上一点且AD=4,E为线段CD上一点,满足∠EAC=∠BAC,则AE=2.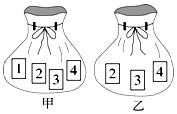 如图,甲袋内共有4张牌,牌面分别标记数字1,2,3,4;乙袋内共有3张牌,牌面分别标记数字2,3,4.甲袋中每张牌被取出的机会相等,且乙袋中每张牌被取出的机会也相等.分别从甲乙两袋中各随机抽取一张牌,请用列表或画树形图的方法,求抽出的两张牌面上的数字之和大于6的概率.
如图,甲袋内共有4张牌,牌面分别标记数字1,2,3,4;乙袋内共有3张牌,牌面分别标记数字2,3,4.甲袋中每张牌被取出的机会相等,且乙袋中每张牌被取出的机会也相等.分别从甲乙两袋中各随机抽取一张牌,请用列表或画树形图的方法,求抽出的两张牌面上的数字之和大于6的概率.
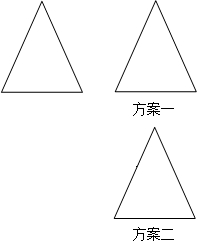 张倩同学打算制作一个平行四边形纸板,但手中只有一块等腰三角形纸板.张倩同学想了一下,用剪刀只剪了一刀,便得到一个平行四边形,且纸板充分利用没有浪费.你知道张倩是怎样剪的吗?用虚线表示出剪刀线;并请你画出两种张倩所拼的平行四边形.
张倩同学打算制作一个平行四边形纸板,但手中只有一块等腰三角形纸板.张倩同学想了一下,用剪刀只剪了一刀,便得到一个平行四边形,且纸板充分利用没有浪费.你知道张倩是怎样剪的吗?用虚线表示出剪刀线;并请你画出两种张倩所拼的平行四边形.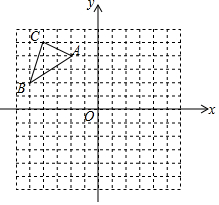 已知△ABC在平面直角坐标系中的位置如图所示.将△ABC向右平移6个单位长度,再向下平移6个单位长度得到△A1B1C1.(图中每个小方格边长均为1个单位长度).
已知△ABC在平面直角坐标系中的位置如图所示.将△ABC向右平移6个单位长度,再向下平移6个单位长度得到△A1B1C1.(图中每个小方格边长均为1个单位长度).