题目内容
5.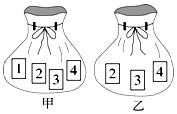 如图,甲袋内共有4张牌,牌面分别标记数字1,2,3,4;乙袋内共有3张牌,牌面分别标记数字2,3,4.甲袋中每张牌被取出的机会相等,且乙袋中每张牌被取出的机会也相等.分别从甲乙两袋中各随机抽取一张牌,请用列表或画树形图的方法,求抽出的两张牌面上的数字之和大于6的概率.
如图,甲袋内共有4张牌,牌面分别标记数字1,2,3,4;乙袋内共有3张牌,牌面分别标记数字2,3,4.甲袋中每张牌被取出的机会相等,且乙袋中每张牌被取出的机会也相等.分别从甲乙两袋中各随机抽取一张牌,请用列表或画树形图的方法,求抽出的两张牌面上的数字之和大于6的概率.
分析 首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两张牌面上的数字之和大于6的情况,然后利用概率公式求解即可求得答案.
解答 解:画树状图得:
由树形图可知所有可能的结果有12种,两张牌面上的数字之和大于6的情况有3种,
所以P(和大于6)=$\frac{3}{12}$=$\frac{1}{4}$.
点评 本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
10. 如图,在平面直角坐标系中,∠AOB=30°,点A的坐标为(2,0),过点A作AA1⊥OB,垂足为点A1,过A1作A1A2⊥x轴,垂足为点A2;再过点A2作A2A3⊥OB,垂足为点A3;再过点A3作A3A4⊥x轴,垂足为点A4…;这样一直作下去,则A2017的横坐标为( )
如图,在平面直角坐标系中,∠AOB=30°,点A的坐标为(2,0),过点A作AA1⊥OB,垂足为点A1,过A1作A1A2⊥x轴,垂足为点A2;再过点A2作A2A3⊥OB,垂足为点A3;再过点A3作A3A4⊥x轴,垂足为点A4…;这样一直作下去,则A2017的横坐标为( )
 如图,在平面直角坐标系中,∠AOB=30°,点A的坐标为(2,0),过点A作AA1⊥OB,垂足为点A1,过A1作A1A2⊥x轴,垂足为点A2;再过点A2作A2A3⊥OB,垂足为点A3;再过点A3作A3A4⊥x轴,垂足为点A4…;这样一直作下去,则A2017的横坐标为( )
如图,在平面直角坐标系中,∠AOB=30°,点A的坐标为(2,0),过点A作AA1⊥OB,垂足为点A1,过A1作A1A2⊥x轴,垂足为点A2;再过点A2作A2A3⊥OB,垂足为点A3;再过点A3作A3A4⊥x轴,垂足为点A4…;这样一直作下去,则A2017的横坐标为( )| A. | $\frac{3}{2}$•($\frac{\sqrt{3}}{2}$)2015 | B. | $\frac{3}{2}$•($\frac{\sqrt{3}}{2}$)2016 | C. | $\frac{3}{2}$•($\frac{\sqrt{3}}{2}$)2017 | D. | $\frac{3}{2}$•($\frac{\sqrt{3}}{2}$)2018 |
17.若k≠0,b>0,则y=kx+b的图象可能是( )
| A. | 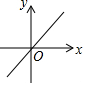 | B. | 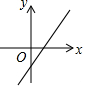 | C. | 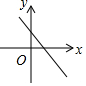 | D. | 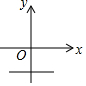 |
15. 己知实数a,b在数轴上的位置如图所示,下列结论错误的是( )
己知实数a,b在数轴上的位置如图所示,下列结论错误的是( )
 己知实数a,b在数轴上的位置如图所示,下列结论错误的是( )
己知实数a,b在数轴上的位置如图所示,下列结论错误的是( )| A. | 1<|a|<b | B. | 1<-a<b | C. | |a|<1<|b| | D. | -b<a<-1 |
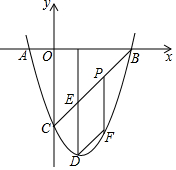 如图,抛物线y=x2+bx+c与x轴相交于A、B两点,点B的坐标为(3,0),与y轴相交于点C(0,-3),顶点为D.
如图,抛物线y=x2+bx+c与x轴相交于A、B两点,点B的坐标为(3,0),与y轴相交于点C(0,-3),顶点为D.
 如图,在平面直角坐标系中,△ABC的三个顶点分别为A(-4,3),B(-1,2),C(-2,1)
如图,在平面直角坐标系中,△ABC的三个顶点分别为A(-4,3),B(-1,2),C(-2,1)