题目内容
已知代数式(
-
)÷
.请解答下列问题:
(1)当x=2sin30°+tan60°时,求原代数式的值;
(2)当x在实数范围内取值时,原代数式的值能等于-1吗?说明理由.
| 2x2+2x |
| x2-1 |
| x2-x |
| x2-2x+1 |
| x |
| x+1 |
(1)当x=2sin30°+tan60°时,求原代数式的值;
(2)当x在实数范围内取值时,原代数式的值能等于-1吗?说明理由.
考点:分式的化简求值,特殊角的三角函数值
专题:
分析:(1)先根据分式混合运算的法则把原式进行化简,再求出x的值代入进行计算即可;
(2)令(1)中代数式的值等于-1,求出x的值,代入公分母进行检验即可.
(2)令(1)中代数式的值等于-1,求出x的值,代入公分母进行检验即可.
解答:解:(1)原式=[
-
]•
=
•
=
,
当x=sin30°+tan60°=1+
时,原式=
=
;
(2)不能.
理由:当
=-1时,去分母得,x+1=-x+1,解得x=0,
检验:当x=0时,x(x-1)(x+1)=0,
故代数式的值不能为0.
| 2x(x+1) |
| (x+1)(x-1) |
| x(x-1) |
| (x-1)2 |
| x+1 |
| x |
=
| x |
| x-1 |
| x+1 |
| x |
=
| x+1 |
| x-1 |
当x=sin30°+tan60°=1+
| 3 |
1+
| ||
1+
|
2
| ||
| 3 |
(2)不能.
理由:当
| x+1 |
| x-1 |
检验:当x=0时,x(x-1)(x+1)=0,
故代数式的值不能为0.
点评:本题考查了分式的化简求值,熟分式混合运算的法则是解题的关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
2014年三月份发生了一件举国悲痛的空难事件--马航失踪,噩耗传来后,国家为了寻救生还者及找到失事飞机,在搜救方面花费了大量的人力物力,若预计需花费用共计8910000000元,用科学记数法表示为( )
| A、8.91×10-9 |
| B、89.1×108 |
| C、8.91×109 |
| D、0.891×1010 |
 如图,一艘轮船位于灯塔C的北偏东30°方向上的A处,且A处距离灯塔C80海里,轮船沿正南方向匀速航行一段时间后,到达灯塔C的东南方向上的B处.
如图,一艘轮船位于灯塔C的北偏东30°方向上的A处,且A处距离灯塔C80海里,轮船沿正南方向匀速航行一段时间后,到达灯塔C的东南方向上的B处.
 如图,分别延长平行四边形ABCD的边CD,AB到E,F使DE=BF=
如图,分别延长平行四边形ABCD的边CD,AB到E,F使DE=BF=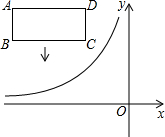 如图,在平面直角坐标系中,反比例函数
如图,在平面直角坐标系中,反比例函数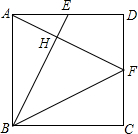 已知:如图,在正方形ABCD中,点E是边AD的中点,联结BE,过点A作AF⊥BE,分别交BE、CD于点H、F,联结BF.
已知:如图,在正方形ABCD中,点E是边AD的中点,联结BE,过点A作AF⊥BE,分别交BE、CD于点H、F,联结BF.