题目内容
4．请叙述三角形的中位线定律，并证明．分析 构造平行四边形来证明三角形的中位线定理．
解答 解：三角形中位线定理：三角形的中位线平行于第三边，且等于第三边的一半．
理由：如图，延 长DE 到 F，使EF=DE，连 结CF、DC、AF
∵AE=CE DE=EF
∴四边形ADCF为平行四边形
∴AD∥CF，AD=CF
∵AD=BD，
∴BD∥CF，BD=CF，
∴四边形BCFD为平行四边形
∴BC∥DF，BC=DF
∴DE∥BC 且 DE=$\frac{1}{2}$BC
点评 此题是三角形中位线定理，主要考查了平行四边形的性质和判定，解本题的关键是构造平行四边形．
练习册系列答案
名校课堂系列答案
相关题目
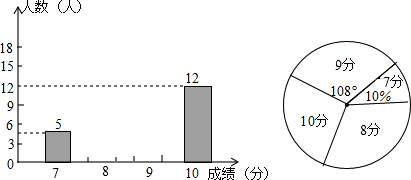
为了了解某校七年级学生完成数学课前预习的惰况，随机抽取该年级100名学生进行了调查，调查结果分为四类：
现在的乐陵已经实现村村通公路，现有两个城镇A、B与两条公路ME，MF位置如图所示，其中ME是东西方向的公路．现电信部门需在C处修建一座信号发射塔，要求发射塔到两个城镇A、B的距离必须相等，到两条公路ME，MF的距离也必须相等，且在∠FME的内部．
如图，在△ABC中，AB=AC，AD⊥BC于点D，E是边AB的中点，连接DE，若AD=12，BC=10，求DE的长．
如图，在平面直角坐标系中，抛物线经过坐标原点O和x轴上另一点E，顶点M的坐标为（2，4），矩形ABCD的顶点A与点O重合，点B、D的坐标分别为（0，3）、（-2，0），将矩形ABCD以每秒1个单位长度的速度沿x轴的正方向平移，同时点P也以每秒a个单位长度从A出发，沿A→B→C→D运动，到点D停止，设矩形移动的时间为t（s）．
13．下列各点在直线y=2x+4上的是（ ）
| A． | （-4，4） | B． | （4，-4） | C． | （-2，-8） | D． | （-2，0） |
