题目内容
20.(1)解方程:$\frac{x}{x-1}$-$\frac{2x-1}{{{x^2}-1}}$=1(2)解方程组:$\left\{{\begin{array}{l}{3x-2y=-1}\\{x+3y=7}\end{array}}$.
分析 (1)把分式方程化为整式方程,再求解.
(2)利用加减消元法解答即可.
解答 解:(1)化为整式方程为:x(x+1)-2x+1=(x+1)(x-1)
解得:x=2,
经检验x=2是原方程的解,
所以原分式方程的解为:x=2;
(2)$\left\{\begin{array}{l}{3x-2y=-1①}\\{x+3y=7②}\end{array}\right.$,
②×3-①得:y=2,
把y=2代入②得:x=1,
所以原方程组的解为:$\left\{{\begin{array}{l}{x=1}\\{y=2}\end{array}}\right.$.
点评 本题考查解分式方程的能力,注意:(1)解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.(2)解分式方程一定注意要验根.

练习册系列答案
相关题目
 如图,在△ABC中,D,E分别是AB,AC的中点,BE=2DE,延长DE到点F,使得EF=2DE,连接CF.判断四边形BCFE的形状,并证明.
如图,在△ABC中,D,E分别是AB,AC的中点,BE=2DE,延长DE到点F,使得EF=2DE,连接CF.判断四边形BCFE的形状,并证明. 已知反比例函数y=$\frac{k}{x}$,经过点E(3,4),现请你在反比例函数y=$\frac{k}{x}$上找出一点P,使∠POE=45°,则此点P的坐标为(2$\sqrt{21}$,$\frac{6\sqrt{21}}{21}$).
已知反比例函数y=$\frac{k}{x}$,经过点E(3,4),现请你在反比例函数y=$\frac{k}{x}$上找出一点P,使∠POE=45°,则此点P的坐标为(2$\sqrt{21}$,$\frac{6\sqrt{21}}{21}$). 如图,矩形ABCD中,AC与BD交于O点,AM∥BD,DM∥AC,AM、DM相交于点M,求证:四边形AODM是菱形.
如图,矩形ABCD中,AC与BD交于O点,AM∥BD,DM∥AC,AM、DM相交于点M,求证:四边形AODM是菱形. 如图,在正方形ABCD中,点E,点F分别在边BC,DC上,BE=DF,∠EAF=60°,点G在DC上,且∠AGC=120°,EG平分∠AGC,连接AG.
如图,在正方形ABCD中,点E,点F分别在边BC,DC上,BE=DF,∠EAF=60°,点G在DC上,且∠AGC=120°,EG平分∠AGC,连接AG.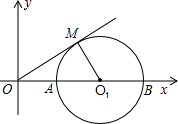 如图,已知半径为1的⊙O1与x轴交于A,B两点,OM为⊙O1的切线,切点为M,圆心O1的坐标为(2,0),二次函数y=-x2+bx+c的图象经过A,B两点.
如图,已知半径为1的⊙O1与x轴交于A,B两点,OM为⊙O1的切线,切点为M,圆心O1的坐标为(2,0),二次函数y=-x2+bx+c的图象经过A,B两点.