题目内容
1.已知抛物线y=-x2+4x+5与x轴交于A、B两点,A在B左侧,顶点为P.(1)求A、B两点的坐标;
(2)求△ABP的面积;
(3)若点C(x1,y1)和点D(x2,y2)在该抛物线上,则当0<x1<x2<1时,请直接写出y1与y2的大小关系.
分析 (1)根据抛物线与x轴相交,即y=0,解一元二次方程即可;
(2)根据顶点坐标公式,求出顶点坐标,再根据三角形的面积公式计算即可;
(3)根据抛物线的增减性,直接判断即可.
解答 解:(1)令y=0,得:-x2+4x+5=0,
解得:x1=-1,x2=5,
∵点A在点B的左边,
∴点A(-1,0),点B(5,0);
(2)∵a=-1,b=4,c=5,
∴$-\frac{b}{2a}=-\frac{4}{-2}=2$,$\frac{4ac-{b}^{2}}{4a}=\frac{4×(-1)×5-{4}^{2}}{4×(-1)}=\frac{-20-16}{-4}=9$,
∴点P(2,9),
∴${S}_{△ABC}=\frac{1}{2}×(5+1)×9=27$;
(3)y2>y1.
理由:∵a=-1<0,对称轴为x=2,
∴当0<x1<x2<1时,y随x的增大而增大,
∴y2>y1.
点评 本题主要考查抛物线与x轴的交点,顶点坐标公式及抛物线的增减性,熟记相关的公式是解决此题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
9.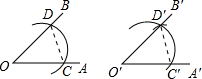 尺规作图作一个等于已知角的示意图如图,则要说明∠D′O′C′=∠DOC,需要证明△D′O′C′≌△DOC,则这两个三角形全等的依据是( )
尺规作图作一个等于已知角的示意图如图,则要说明∠D′O′C′=∠DOC,需要证明△D′O′C′≌△DOC,则这两个三角形全等的依据是( )
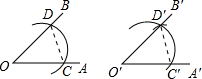 尺规作图作一个等于已知角的示意图如图,则要说明∠D′O′C′=∠DOC,需要证明△D′O′C′≌△DOC,则这两个三角形全等的依据是( )
尺规作图作一个等于已知角的示意图如图,则要说明∠D′O′C′=∠DOC,需要证明△D′O′C′≌△DOC,则这两个三角形全等的依据是( )| A. | SSS | B. | SAS | C. | ASA | D. | AAS |
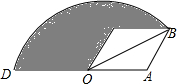 如图,在菱形OABC中,∠C=120°,OA=2,以点O为圆心,OB的长为半径画弧,交OA的延长线于点D,则图中阴影部分的面积为5π-$\sqrt{3}$.
如图,在菱形OABC中,∠C=120°,OA=2,以点O为圆心,OB的长为半径画弧,交OA的延长线于点D,则图中阴影部分的面积为5π-$\sqrt{3}$.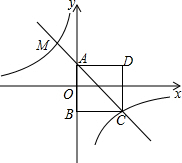 如图,四边形ABCD为正方形,点A的坐标为(0,1),点B的坐标为(0,-2),反比例函数y=$\frac{k}{x}$的图象经过点C,一次函数y=ax+b的图象经过A、C两点.
如图,四边形ABCD为正方形,点A的坐标为(0,1),点B的坐标为(0,-2),反比例函数y=$\frac{k}{x}$的图象经过点C,一次函数y=ax+b的图象经过A、C两点.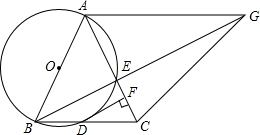 如图,在△ABC中,AB=AC,以AB为直径的圆O交BC于点D,交AC于点E,过点D作DF⊥AC,垂足为F.
如图,在△ABC中,AB=AC,以AB为直径的圆O交BC于点D,交AC于点E,过点D作DF⊥AC,垂足为F.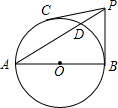 如图,AB是⊙O的直径,PB、PC是⊙O的切线,切点为B、C,连接PA交⊙O于D,∠BPC=2∠A.
如图,AB是⊙O的直径,PB、PC是⊙O的切线,切点为B、C,连接PA交⊙O于D,∠BPC=2∠A.