题目内容
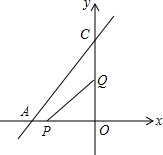 如图,已知直线AC的解析式为y=
如图,已知直线AC的解析式为y=| 4 |
| 3 |
考点:一元二次方程的应用
专题:几何动点问题
分析:首先求得直线与两坐标轴的交点坐标,然后表示出三角形的两边利用三角形的面积计算公式列出方程计算即可.
解答:解:直线y=
x+8与x轴、y轴的交点坐标分别为A(-6,0),B(0,8)
∴OA=6,OB=8
设P、Q移动的时间为x秒.
根据题意得
•2x•(6-x)=8,
整理得x2-6x+8=0,
∴x=2或x=4,
当x=2时,AP=2,OQ=4,P、Q分别在OA、OC上,符合题意.
当x=4时,AP=4,OQ=8,此时Q点与C点重合,同样符合题意.
答:经过2秒或4秒时,能使△PQO的面积为8个平方单位.
| 4 |
| 3 |
∴OA=6,OB=8
设P、Q移动的时间为x秒.
根据题意得
| 1 |
| 2 |
整理得x2-6x+8=0,
∴x=2或x=4,
当x=2时,AP=2,OQ=4,P、Q分别在OA、OC上,符合题意.
当x=4时,AP=4,OQ=8,此时Q点与C点重合,同样符合题意.
答:经过2秒或4秒时,能使△PQO的面积为8个平方单位.
点评:本题考查了一元二次方程的应用,解题的关键是能够根据直线的解析式确定直线与两坐标轴的交点,从而求得有关的线段的长,难度不大.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
 如图所示,铁路的路基横断面是等腰梯形,斜坡AB的坡度为1:
如图所示,铁路的路基横断面是等腰梯形,斜坡AB的坡度为1: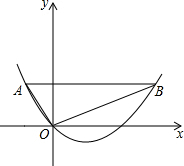 如图,在平面直的坐标角坐标系中,已知点A为(-1,
如图,在平面直的坐标角坐标系中,已知点A为(-1,