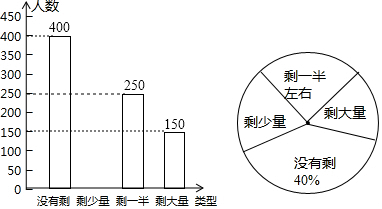
题目内容
19.已知方程组$\left\{\begin{array}{l}{x+2y=3a}\\{3x-y=a}\end{array}\right.$,若a≠0,则$\frac{x}{y}$=$\frac{5}{8}$.分析 应用加减法,求出方程组的解是多少,即可求出$\frac{x}{y}$的值是多少.
解答 解:$\left\{\begin{array}{l}{x+2y=3a①}\\{3x-y=a②}\end{array}\right.$
①+②×2,可得:7x=5a,
解得x=$\frac{5}{7}a$,
把x=$\frac{5}{7}a$代入②,
解得y=$\frac{8}{7}$a,
∵a≠0,
∴$\frac{x}{y}$=$\frac{\frac{5}{7}a}{\frac{8}{7}a}$=$\frac{5}{8}$.
故答案为:$\frac{5}{8}$.
点评 此题主要考查了解二元一次方程组的方法,要熟练掌握,注意加减法和代入法的应用.

练习册系列答案
相关题目
9.骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场,某车行经营的A型车去年3月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售价比去年增加400元,若今年3月份与去年3月份卖出的A型车数量相同,则今年3月份A型车销售总额将比去年3月份销售总额增加25%.
(1)求今年3月份A型车每辆销售价多少元?
(2)该车行计划今年4月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,A、B两种型号车的进货和销售价格如下表,问应如何进货才能使这批车获利最多?
(1)求今年3月份A型车每辆销售价多少元?
(2)该车行计划今年4月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,A、B两种型号车的进货和销售价格如下表,问应如何进货才能使这批车获利最多?
| A型车 | B型车 | |
| 进货价格(元/辆) | 1100 | 1400 |
| 销售价格(元/辆) | 今年的销售价格 | 2400 |
9.为解决“最后一公里”的交通接驳问题,平谷区投放了大量公租自行车供市民使用.据统计,目前我区共有公租自行车3 500辆.将3 500用科学记数法表示应为( )
| A. | 0.35×104 | B. | 3.5×103 | C. | 3.5×102 | D. | 35×102 |
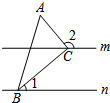 如图,直线m∥n,△ABC的顶点B,C分别在直线n,m上,且∠ACB=90°,若∠1=40°,则∠2等于130度.
如图,直线m∥n,△ABC的顶点B,C分别在直线n,m上,且∠ACB=90°,若∠1=40°,则∠2等于130度.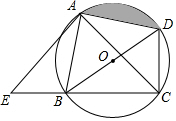 如图,四边形ABCD内接于⊙O,且BD为直径,∠ACB=45°,过A点的AC的垂线交BC的延长线于点E.
如图,四边形ABCD内接于⊙O,且BD为直径,∠ACB=45°,过A点的AC的垂线交BC的延长线于点E.