题目内容
1.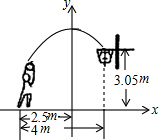 如图,运动员甲在距篮下4m处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为2.5m时,达到最大高度3.5米,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05米.
如图,运动员甲在距篮下4m处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为2.5m时,达到最大高度3.5米,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05米.(1)建立如图所示的直角坐标系,求抛物线的解析式.
(2)该运动员身高1.8米,在这次跳投中,球在头顶上方0.25米处出手,问:球出手时,他跳离地面的高度是多少?
(3)运动员乙跳离地面时,最高能摸到3.3m,问:在(2)的条件下,运动员乙在运动员甲与篮板之间的什么范围内能在空中截住球?
分析 (1)设抛物线的表达式为y=ax2+3.5,依题意可知图象经过的坐标,由此可得a的值.
(2)设球出手时,他跳离地面的高度为hm,则可得h+2.05=-0.2×(-2.5)2+3.5.
(3)当y=3.3m,进而代入函数解析式,求出x的值,即可得出答案.
解答 解:(1)∵当球运行的水平距离为2.5米时,达到最大高度3.5米,
∴抛物线的顶点坐标为(0,3.5),
∴设抛物线的表达式为y=ax2+3.5.
由图知图象过以下点:(1.5,3.05).
∴2.25a+3.5=3.05,
解得:a=-0.2,
∴抛物线的表达式为y=-0.2x2+3.5.
(2)设球出手时,他跳离地面的高度为hm,
因为(1)中求得y=-0.2x2+3.5,
则球出手时,球的高度为h+1.8+0.25=(h+2.05)m,
∴h+2.05=-0.2×(-2.5)2+3.5,
∴h=0.2(m).
答:球出手时,他跳离地面的高度为0.2m.
(3)由题意可得出:y=3.3,
则3.3=-0.2x2+3.5
解得:x1=1,x2=-1,
∴4-1=3(m),
∴乙在距离甲3米范围内或离篮板0.5米的范围内能在空中截住球.
点评 此题主要考查了二次函数的应用,建立合适的平面直角坐标系是解决本题的突破点,求得球出手时距离地面的高度是解决本题的关键.

练习册系列答案
相关题目
11.下列图形中是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
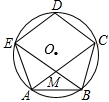 如图,正五边形ABCDE的对角线AC,BE相交于M,求证:四边形CDEM是菱形.
如图,正五边形ABCDE的对角线AC,BE相交于M,求证:四边形CDEM是菱形. 如图,在△ABC中,AB=6,BC=AC=5.
如图,在△ABC中,AB=6,BC=AC=5.