题目内容
13.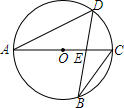 如图,AC是⊙O的直径,AC=10,弦BD交AC于点E.
如图,AC是⊙O的直径,AC=10,弦BD交AC于点E.(1)求证:△ADE∽△BCE;
(2)若E是BD中点,求AD2+BC2的值.
分析 (1)根据圆周角定理求出∠A=∠B,根据相似三角形的判定推出即可;
(2)连接CD,根据圆周角定理得到∠ADC=90°,根据垂径定理得到AC⊥BD,BE=DE,由射影定理得到DE2=BE2=AE.CE,∠AEC=∠BEC=90°,等量代换即可得到结论.
解答 证明:(1)∵弧CD=弧CD,
∴∠A=∠B,
又∵∠AED=∠BEC,
∴△ADE∽△BCE;
(2)连接CD,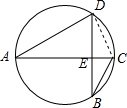
∵AC是⊙O的直径,
∴∠ADC=90°,
∵E是BD中点,AC是⊙的直径
∴AC⊥BD,BE=DE,
∴DE2=BE2=AE.CE,∠AEC=∠BEC=90°,
∴AD2+BC2=DE2+AE2+CE2+BE2=2DE2+AE2+CE2=AE2+CE2+2AE.CE=(AE+CE)2=100.
点评 本题考查了圆周角定理,相似三角形的判定,垂径定理,完全平方公式,射影定理,主要考查学生运用定理进行推理的能力,题目比较好,难度适中.

练习册系列答案
相关题目
8. 如图所示的暗礁区,两灯塔A,B之间的距离恰好等于圆半径的$\sqrt{2}$倍,为了使航船(S)不进入暗礁区,那么S 对两灯塔A,B的视角∠ASB必须( )
如图所示的暗礁区,两灯塔A,B之间的距离恰好等于圆半径的$\sqrt{2}$倍,为了使航船(S)不进入暗礁区,那么S 对两灯塔A,B的视角∠ASB必须( )
 如图所示的暗礁区,两灯塔A,B之间的距离恰好等于圆半径的$\sqrt{2}$倍,为了使航船(S)不进入暗礁区,那么S 对两灯塔A,B的视角∠ASB必须( )
如图所示的暗礁区,两灯塔A,B之间的距离恰好等于圆半径的$\sqrt{2}$倍,为了使航船(S)不进入暗礁区,那么S 对两灯塔A,B的视角∠ASB必须( )| A. | 大于60° | B. | 小于60° | C. | 大于45° | D. | 小于45° |
5.一架5m长的梯子斜靠在一竖直的墙上,这时梯脚距离墙角3m,如果梯子的顶端沿墙下滑1m,那么梯脚移动的距离是( )
| A. | 0.5m | B. | 0.8m | C. | 1m | D. | 1.2m |
 如图,∠B=∠D=90°,OA=OC.当添加条件OB=OD时,就可以得到△ABO≌△CDO,此时的依据是HL.
如图,∠B=∠D=90°,OA=OC.当添加条件OB=OD时,就可以得到△ABO≌△CDO,此时的依据是HL.