题目内容
17.在Rt△ABC中,∠C=90°,AB=2BC,AC2=27,求AB的长.分析 直接利用勾股定理AC2+BC2=AB2,进而求出答案.
解答  解:如图所示:
解:如图所示:
∵∠C=90°,AB=2BC,AC2=27,
∴AC2+BC2=AB2,
∴27+BC2=(2BC)2,
解得:BC=3,
∴AB=6.
点评 此题主要考查了勾股定理,正确应用已知是解题关键.

练习册系列答案
 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
5. 如图,在x轴上有两点A(-3,0)和B(3,0),有一动点C在线段AB上从点A运动到点B(不与A,B重合),分别以AC,BC为底边作等腰△AEC和等腰△BFC,顶点E,F恰好落在反比例函数y=-$\frac{5}{x}$(x<0)和y=$\frac{2}{x}$(x>0)的图象上,连结EF,在整个运动过程中,线段EF长度的变化情况是( )
如图,在x轴上有两点A(-3,0)和B(3,0),有一动点C在线段AB上从点A运动到点B(不与A,B重合),分别以AC,BC为底边作等腰△AEC和等腰△BFC,顶点E,F恰好落在反比例函数y=-$\frac{5}{x}$(x<0)和y=$\frac{2}{x}$(x>0)的图象上,连结EF,在整个运动过程中,线段EF长度的变化情况是( )
 如图,在x轴上有两点A(-3,0)和B(3,0),有一动点C在线段AB上从点A运动到点B(不与A,B重合),分别以AC,BC为底边作等腰△AEC和等腰△BFC,顶点E,F恰好落在反比例函数y=-$\frac{5}{x}$(x<0)和y=$\frac{2}{x}$(x>0)的图象上,连结EF,在整个运动过程中,线段EF长度的变化情况是( )
如图,在x轴上有两点A(-3,0)和B(3,0),有一动点C在线段AB上从点A运动到点B(不与A,B重合),分别以AC,BC为底边作等腰△AEC和等腰△BFC,顶点E,F恰好落在反比例函数y=-$\frac{5}{x}$(x<0)和y=$\frac{2}{x}$(x>0)的图象上,连结EF,在整个运动过程中,线段EF长度的变化情况是( )| A. | 一直增大 | B. | 一直减小 | C. | 先增大后减小 | D. | 先减小后增大 |
2.方程组$\left\{\begin{array}{l}{x+y=1}\\{2x+y=5}\end{array}\right.$的解为( )
| A. | $\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-2}\\{y=3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=4}\\{y=-3}\end{array}\right.$ |
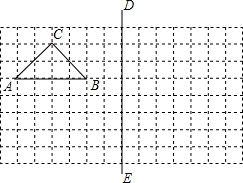 如图,在所给网络图(每小格均为边长是1的正方形)中完成下列各题:
如图,在所给网络图(每小格均为边长是1的正方形)中完成下列各题:
 如图,△ABC中,∠C=90°,AC=3cm,BC=6cm,动点P从点B出发以2cm/s的速度向点C移动,动点Q从C出发以1cm/s的速度向点A移动,如果动点P、Q同时出发,要使△CBA与C、P、Q三点构成的三角形相似,求所需要的时间是多少秒?
如图,△ABC中,∠C=90°,AC=3cm,BC=6cm,动点P从点B出发以2cm/s的速度向点C移动,动点Q从C出发以1cm/s的速度向点A移动,如果动点P、Q同时出发,要使△CBA与C、P、Q三点构成的三角形相似,求所需要的时间是多少秒?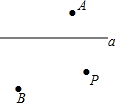 如图,平面上有直线a及直线a外的三点A、B、P.
如图,平面上有直线a及直线a外的三点A、B、P. 在20km的越野比赛中,甲乙两选手均跑完全程,他们的行程y(单位:km)随时间x(单位:h)变化的图象如图所示,根据图中提供的信息,解答下列问题:
在20km的越野比赛中,甲乙两选手均跑完全程,他们的行程y(单位:km)随时间x(单位:h)变化的图象如图所示,根据图中提供的信息,解答下列问题: