题目内容
12. 如图,△ABC中,∠C=90°,AC=3cm,BC=6cm,动点P从点B出发以2cm/s的速度向点C移动,动点Q从C出发以1cm/s的速度向点A移动,如果动点P、Q同时出发,要使△CBA与C、P、Q三点构成的三角形相似,求所需要的时间是多少秒?
如图,△ABC中,∠C=90°,AC=3cm,BC=6cm,动点P从点B出发以2cm/s的速度向点C移动,动点Q从C出发以1cm/s的速度向点A移动,如果动点P、Q同时出发,要使△CBA与C、P、Q三点构成的三角形相似,求所需要的时间是多少秒?
分析 若两三角形相似,则由相似三角形性质可知,其对应边成比例,据此可解出两三角形相似时所需时间.
解答 解:设经过t秒后两三角形相似,则可分下列两种情况进行求解,
①若Rt△ABC∽Rt△QPC则$\frac{AC}{BC}$=$\frac{QC}{PC}$,即$\frac{3}{6}$=$\frac{t}{6-2t}$,解之得t=1.5;
②若Rt△ABC∽Rt△PQC则$\frac{PC}{QC}$=$\frac{AC}{BC}$,$\frac{6-2t}{t}$=$\frac{3}{6}$,解之得t=2.4;
由P点在BC边上的运动速度为2cm/s,Q点在AC边上的速度为1cm/s,可求出t的取值范围应该为0<t<3,
验证可知①②两种情况下所求的t均满足条件.所以可知要使△CPQ与△CBA相似,所需要的时间为1.5或2.4秒.
点评 本题综合考查了相似三角形的性质以及一元一次方程的应用问题,并且需要用到分类讨论的思想,解题时应注意解答后的验证.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.如图,AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的度数是( )


| A. | 60° | B. | 50° | C. | 40° | D. | 30° |
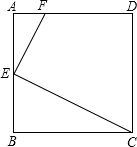 如图,已知正方形ABCD中,AB=a,点E为AB的中点,点F在AD边上,且AF=$\frac{1}{4}$AD,试说明EF⊥CE.
如图,已知正方形ABCD中,AB=a,点E为AB的中点,点F在AD边上,且AF=$\frac{1}{4}$AD,试说明EF⊥CE. 定义新运算:对于任意实数a,b,都有a⊕b=a(a-b)+a,等式右边是通常的加法、减法及乘法运算,比如:2⊕5=2×(2-5)+2=2×(-3)+2=-6+2=4.
定义新运算:对于任意实数a,b,都有a⊕b=a(a-b)+a,等式右边是通常的加法、减法及乘法运算,比如:2⊕5=2×(2-5)+2=2×(-3)+2=-6+2=4. 如图,在四边形ABCD中,AD⊥DC,AD=8,DC=6,CB=24,AB=26,求四边形ABCD的面积.
如图,在四边形ABCD中,AD⊥DC,AD=8,DC=6,CB=24,AB=26,求四边形ABCD的面积.