题目内容
 阅读以下内容,并回答问题:
阅读以下内容,并回答问题:若一个三角形的两边平方和等于第三边平方的两倍,我们称这样的三角形为奇异三角形.
(1)命题“等边三角形一定是奇异三角形”是
(2)在△ABC中,已知∠C=90°,△ABC的内角∠A、∠B、∠C所对边的长分别为a、b、c,且b>a,若Rt△ABC是奇异三角形,求a:b:c;
(3)如图,已知AB是⊙O的直径,C是⊙O上一点(点C与点A、B不重合),D是半圆
 |
| ADB |
考点:圆心角、弧、弦的关系,勾股定理
专题:阅读型
分析:(1)直接根据奇异三角形的定义直接得出结论;
(2)先根据勾股定理得出a2+b2=c2,再由Rt△ABC是奇异三角形,且b>a可知a2+c2=2b2,把a当作已知条件表示出b,c的值,进而可得出结论;
(3)连接BD,根据圆周角定理得出∠ACB=∠ADB=90°,在Rt△ACB与在Rt△ADB中可得出AC2+BC2=AB2,AD2+BD2=AB2,根据点D是半圆
的中点,得出
=
.故可得出AD=BD.通过等量代换可得出AC2+CB2=2AD2.再由CB=CE,AE=AD可得出AC2+CE2=2AE2故可得出结论.
(2)先根据勾股定理得出a2+b2=c2,再由Rt△ABC是奇异三角形,且b>a可知a2+c2=2b2,把a当作已知条件表示出b,c的值,进而可得出结论;
(3)连接BD,根据圆周角定理得出∠ACB=∠ADB=90°,在Rt△ACB与在Rt△ADB中可得出AC2+BC2=AB2,AD2+BD2=AB2,根据点D是半圆
 |
| ADB |
 |
| AD |
 |
| BD |
解答: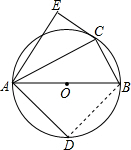 解:(1)∵若一个三角形的两边平方和等于第三边平方的两倍,我们称这样的三角形为奇异三角形,
解:(1)∵若一个三角形的两边平方和等于第三边平方的两倍,我们称这样的三角形为奇异三角形,
∴等边三角形一定是奇异三角形是真命题.
故答案为:真;
(2)∵∠C=90°,
∴a2+b2=c2①.
∵Rt△ABC是奇异三角形,且b>a,
∴a2+c2=2b2②.
由①②得:b=
a,c=
a.
∴a:b:c=1:
:
.
(3)连接BD.
∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°.
在Rt△ACB中,AC2+BC2=AB2,
在Rt△ADB中,AD2+BD2=AB2,
∵点D是半圆
的中点,∴
=
.
∴AD=BD.
∴AB2=AD2+BD2=2AD2.
∴AC2+CB2=2AD2.
又∵CB=CE,AE=AD,
∴AC2+CE2=2AE2.
∴△ACE是奇异三角形.
 解:(1)∵若一个三角形的两边平方和等于第三边平方的两倍,我们称这样的三角形为奇异三角形,
解:(1)∵若一个三角形的两边平方和等于第三边平方的两倍,我们称这样的三角形为奇异三角形,∴等边三角形一定是奇异三角形是真命题.
故答案为:真;
(2)∵∠C=90°,
∴a2+b2=c2①.
∵Rt△ABC是奇异三角形,且b>a,
∴a2+c2=2b2②.
由①②得:b=
| 2 |
| 3 |
∴a:b:c=1:
| 2 |
| 3 |
(3)连接BD.
∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°.
在Rt△ACB中,AC2+BC2=AB2,
在Rt△ADB中,AD2+BD2=AB2,
∵点D是半圆
 |
| ADB |
 |
| AD |
 |
| BD |
∴AD=BD.
∴AB2=AD2+BD2=2AD2.
∴AC2+CB2=2AD2.
又∵CB=CE,AE=AD,
∴AC2+CE2=2AE2.
∴△ACE是奇异三角形.
点评:本题考查的是奇异三角形的定义,熟知勾股定理及等边三角形的性质是解答此题的关键.

练习册系列答案
相关题目
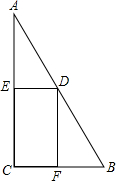 如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,点D是AB上的一个动点(不与A、B两点重合),DE⊥AC于点E,DF⊥BC于点F,点D从靠近点A的某一点向点B移动,矩形DECF的周长变化情况是( )
如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,点D是AB上的一个动点(不与A、B两点重合),DE⊥AC于点E,DF⊥BC于点F,点D从靠近点A的某一点向点B移动,矩形DECF的周长变化情况是( )| A、逐渐减小 |
| B、逐渐增大 |
| C、先增大后减小 |
| D、先减小后增大 |
已知二次函数=a(x-2)2+k的图象开口向上,若点M(-2,y1),N(-1,y2),K(8,y3)在二次函数y=a(x-2)2+k的图象上,则下列结论正确的是( )
| A、y1<y2<y3 |
| B、y2<y1<y3 |
| C、y3<y1<y2 |
| D、y1<y3<y2 |
如果一个有理数的绝对值是5,那么这个数一定是( )
| A、5 | B、-5 |
| C、-5或5 | D、以上都不对 |
下列命题是真命题的是( )
| A、三角形的三条高线相交于三角形内一点 |
| B、等腰三角形的中线与高重合 |
| C、对于所有自然数n,n2-3n+7的值都是质数 |
| D、直角三角形中,30°角所对直角边是斜边一半 |
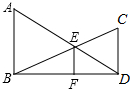 已知,如图所示,AB∥CD,AD交BC于点E,EF∥AB交BD于点F.
已知,如图所示,AB∥CD,AD交BC于点E,EF∥AB交BD于点F. 已知点A和直线m,用尺规作图作出点A关于直线m的轴对称点.
已知点A和直线m,用尺规作图作出点A关于直线m的轴对称点.