题目内容
已知二次函数=a（x-2）2+k的图象开口向上，若点M（-2，y1），N（-1，y2），K（8，y3）在二次函数y=a（x-2）2+k的图象上，则下列结论正确的是（ ）
| A、y1＜y2＜y3 |
| B、y2＜y1＜y3 |
| C、y3＜y1＜y2 |
| D、y1＜y3＜y2 |
考点：二次函数图象上点的坐标特征
专题：
分析：先求出抛物线开口向上，对称轴为直线x=2，然后根据点M、N、K离对称轴的远近求解．
解答：解：∵二次函数y═a（x-2）2+k的图象开口向上，对称轴为直线x=2，
∵M（-2，y1），N（-1，y2），K（8，y3），
∴K点离对称轴最远，N点离对称轴最近，
∴y2＜y1＜y3．
故选B．
∵M（-2，y1），N（-1，y2），K（8，y3），
∴K点离对称轴最远，N点离对称轴最近，
∴y2＜y1＜y3．
故选B．
点评：本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标满足其解析式．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
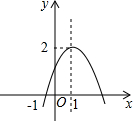如图，已知二次函数y=ax2+bx+c（a≠0）图象过点（-1，0），顶点为（1，2），则结论：①abc＜0；②x=1时，函数的最大值是2；③a+2b+4c＜0；④2a=-b；⑤2c＞3b．其中
正确的结论有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
如果（x-2）（x+3）=x2+px-q，那么p、q的值是（ ）
| A、p=1，q=-6 |
| B、p=5，q=6 |
| C、p=1，q=6 |
| D、p=5，q=-6 |
射线OA，BA分别表示甲、乙两人骑自行车运动过程的一次函数的图象，图中s，t分别表示行驶距离和时间，则下列说法错误的是（ ）| A、当t=4小时时，乙在甲的前面 |
| B、当t=5小时时，甲追上乙 |
| C、甲、乙两人同时同地出发 |
| D、甲的速度比乙的速度更大 |
阅读以下内容，并回答问题：
下列三条线段不能构成直角三角形的是（ ）
| A、32，42，52 | ||||
| B、5，12，13 | ||||
| C、24，25，7 | ||||
D、1，
|
若△ABC∽△A′B′C′，其面积比为1：2，则△ABC与△A′B′C′的相似比为（ ）
| A、1：2 | ||
B、
| ||
| C、1：4 | ||
D、
|
如图所示，在△ABC中，∠A=80°，延长BC到D，∠ABC与∠ACD的平分线相交于A1点，∠A1BC与∠A1CD的平分线相交于A2点，依此类推，∠A4BC与∠A4CD的平分线相交于A5点，则∠A5的度数是