题目内容
5.在矩形ABCD中,AB=4,AD=5,P是射线BC上的一个动点,过点P作PE⊥AP,交射线DC于点E,射线AE交射线BC于点F,当tan∠PAE=$\frac{1}{2}$时,BP的值为3或7.分析 由条件可以证明△ABP∽△PCE,可以得到$\frac{BP}{CE}=\frac{AB}{PC}$=2,再分情况讨论,从而求出a的值.
解答 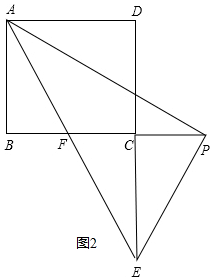 解:设BP=a,如图,根据tan∠PAE=$\frac{1}{2}$,可得:$\frac{AP}{PE}$=2,
解:设BP=a,如图,根据tan∠PAE=$\frac{1}{2}$,可得:$\frac{AP}{PE}$=2,
∵∠APB+∠BPE=90°,∠CEP+∠EPC=90°,
∴∠CEP=∠APB,
又∵∠ABP=∠PCE,
∴△ABP∽△PCE,
∴$\frac{BP}{CE}=\frac{AB}{PC}$=2,
于是:$\frac{a}{EC}=\frac{4}{5-a}$=2 ①或 $\frac{a}{EC}=\frac{4}{a-5}$=2 ②
解得:a=3,EC=1.5或 a=7,EC=3.5.
∴BP=3或7;
故答案为:3或7.
点评 本题考查了相似三角形的判定与性质,矩形的性质,解直角三角形以及勾股定理的运用,利用数形结合得出是解题关键.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
16.设a=2°,b=(-3)2,c=$\root{3}{27}$,d=($\frac{1}{2}$) -1,则a、b、c、d按由小到大的顺序排列正确的是( )
| A. | a<d<c<b | B. | a<b<c<d | C. | d<a<c<b | D. | b<d<c<a |
14.下列语句中,正确的是( )
| A. | 若∠α+∠β=180°,则∠α是补角 | |
| B. | 若∠AOB+∠BOC=180°,则∠AOC是直角 | |
| C. | 若∠α与∠β互为补角,则∠α与∠β中必有一个为锐角,另一个角为钝角 | |
| D. | 若∠α与∠β互为余角,则∠α+∠β=90° |
 如图所示的正方形网格中一共有20个长方形.
如图所示的正方形网格中一共有20个长方形.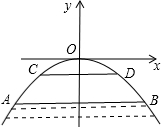 如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20m,如果水位上升3m水面CD的宽是10m.
如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20m,如果水位上升3m水面CD的宽是10m. 如图,在平面直角坐标系xOy中,已知A(1,2),B(3,5),C(6,3),求△ABC的面积.
如图,在平面直角坐标系xOy中,已知A(1,2),B(3,5),C(6,3),求△ABC的面积.