题目内容
等腰直角△ABC,AC=BC,∠ACB=90°,点D为斜边AB中点,以点D为顶点作∠EDF=90°,角的两边分别与两直角边交于点E,F,连接EF.
探究:(1)如图(1)当DE⊥AC时,猜想线段AE、BF、EF长度之间的关系,并加以证明.
(2)如图(2)当DE不与AC垂直时(1)的结论是否存在,并加以证明;
(3)若∠EDF的两边分别与AC延长线、CB延长线交于点E,F连接EF,利用备用图画出图形,直接写出线段AE、BF、EF长度之间的关系(不用证明).

探究:(1)如图(1)当DE⊥AC时,猜想线段AE、BF、EF长度之间的关系,并加以证明.
(2)如图(2)当DE不与AC垂直时(1)的结论是否存在,并加以证明;
(3)若∠EDF的两边分别与AC延长线、CB延长线交于点E,F连接EF,利用备用图画出图形,直接写出线段AE、BF、EF长度之间的关系(不用证明).

分析:(1)AE2+BF2=EF2,理由为:连接CD,如图1所示,由三角形ABC为等腰直角三角形,得到AD=CD,且∠A=∠DCF=45°,再由∠EDF=90°,利用同角的余角相等得到一对角相等,利用ASA得出三角形ADE与三角形CDF全等,利用全等三角形的对应边相等得到AE=CF,再由AC=BC,得到CE=BF,在直角三角形CEF中,利用勾股定理列车关系式,等量代换即可得证;
(2)如图(2)当DE不与AC垂直时(1)的结论存在,利用为:连接CD,如图2所示,由三角形ABC为等腰直角三角形,得到AD=CD,且∠A=∠DCF=45°,再由∠EDF=90°,利用同角的余角相等得到一对角相等,利用ASA得出三角形ADE与三角形CDF全等,利用全等三角形的对应边相等得到AE=CF,再由AC=BC,得到CE=BF,在直角三角形CEF中,利用勾股定理列车关系式,等量代换即可得证;
(3)三线段之间的关系是AE2+BF2=EF2,理由为:连接接CD,如图所示,由三角形ABC为等腰直角三角形,得到AD=CD=BD,且∠ACD=∠ABC=45°,得到一对邻补角相等,再由∠EDF=90°,利用同角的余角相等得到一对角相等,利用ASA得出三角形CDE与三角形BDF全等,利用全等三角形的对应边相等得到CE=BF,得到CE=BF,在直角三角形CEF中,利用勾股定理列车关系式,等量代换即可得证.
(2)如图(2)当DE不与AC垂直时(1)的结论存在,利用为:连接CD,如图2所示,由三角形ABC为等腰直角三角形,得到AD=CD,且∠A=∠DCF=45°,再由∠EDF=90°,利用同角的余角相等得到一对角相等,利用ASA得出三角形ADE与三角形CDF全等,利用全等三角形的对应边相等得到AE=CF,再由AC=BC,得到CE=BF,在直角三角形CEF中,利用勾股定理列车关系式,等量代换即可得证;
(3)三线段之间的关系是AE2+BF2=EF2,理由为:连接接CD,如图所示,由三角形ABC为等腰直角三角形,得到AD=CD=BD,且∠ACD=∠ABC=45°,得到一对邻补角相等,再由∠EDF=90°,利用同角的余角相等得到一对角相等,利用ASA得出三角形CDE与三角形BDF全等,利用全等三角形的对应边相等得到CE=BF,得到CE=BF,在直角三角形CEF中,利用勾股定理列车关系式,等量代换即可得证.
解答: 解:(1)AE2+BF2=EF2,理由为:
解:(1)AE2+BF2=EF2,理由为:
连接CD,
∵AC=BC,∠ACB=90°,D为AB的中点,
∴CD=AD=BD=
AB,∠A=∠DCF=45°,
∵∠ADE+∠CDE=90°,
又∠EDF=90°,
∴∠EDC+∠CDF=90°,
∴∠ADE=∠CDF,
在△ADE和△CDF中,
,
∴△ADE≌△CDF(ASA),
∴AE=CF,又AC=BC,
∴AC-AE=BC-CF,即CE=BF,
在Rt△CEF中,根据勾股定理得:CE2+CF2=EF2,
则AE2+BF2=EF2;
(2)如图(2)当DE不与AC垂直时(1)的结论成立,理由为:
连接CD,
∵AC=BC,∠ACB=90°,D为AB的中点,
∴CD=AD=BD=
AB,∠A=∠DCF=45°,
∵∠ADE+∠CDE=90°,
又∠EDF=90°,
∴∠EDC+∠CDF=90°,
∴∠ADE=∠CDF,
在△ADE和△CDF中,
,
∴△ADE≌△CDF(ASA),
∴AE=CF,又AC=BC,
∴AC-AE=BC-CF,即CE=BF,
在Rt△CEF中,根据勾股定理得:CE2+CF2=EF2,
则AE2+BF2=EF2;
(3)根据题意画出相应的图形,如图所示:
连接CD,
∵AC=BC,∠ACB=90°,D为AB的中点,
∴CD=AD=BD=
AB,∠ACD=∠ABC=45°,
∴∠ECD=∠FBD=135°,
∵∠CDE+∠EDB=90°,
又∠EDF=90°,
∴∠EDB+∠BDF=90°,
∴∠CDE=∠BDF,
在△CDE和△BDF中,
,
∴△CDE≌△BDF(ASA),
∴CE=BF,又AC=BC,
∴CF=BC+BF=AC+CE=AE,
在Rt△CEF中,根据勾股定理得:CE2+CF2=EF2,
则AE2+BF2=EF2.
 解:(1)AE2+BF2=EF2,理由为:
解:(1)AE2+BF2=EF2,理由为:连接CD,
∵AC=BC,∠ACB=90°,D为AB的中点,
∴CD=AD=BD=
| 1 |
| 2 |
∵∠ADE+∠CDE=90°,
又∠EDF=90°,
∴∠EDC+∠CDF=90°,
∴∠ADE=∠CDF,
在△ADE和△CDF中,
|
∴△ADE≌△CDF(ASA),
∴AE=CF,又AC=BC,
∴AC-AE=BC-CF,即CE=BF,
在Rt△CEF中,根据勾股定理得:CE2+CF2=EF2,
则AE2+BF2=EF2;
(2)如图(2)当DE不与AC垂直时(1)的结论成立,理由为:
连接CD,
∵AC=BC,∠ACB=90°,D为AB的中点,
∴CD=AD=BD=
| 1 |
| 2 |
∵∠ADE+∠CDE=90°,
又∠EDF=90°,
∴∠EDC+∠CDF=90°,
∴∠ADE=∠CDF,
在△ADE和△CDF中,
|
∴△ADE≌△CDF(ASA),
∴AE=CF,又AC=BC,
∴AC-AE=BC-CF,即CE=BF,
在Rt△CEF中,根据勾股定理得:CE2+CF2=EF2,
则AE2+BF2=EF2;
(3)根据题意画出相应的图形,如图所示:

连接CD,
∵AC=BC,∠ACB=90°,D为AB的中点,
∴CD=AD=BD=
| 1 |
| 2 |
∴∠ECD=∠FBD=135°,
∵∠CDE+∠EDB=90°,
又∠EDF=90°,
∴∠EDB+∠BDF=90°,
∴∠CDE=∠BDF,
在△CDE和△BDF中,
|
∴△CDE≌△BDF(ASA),
∴CE=BF,又AC=BC,
∴CF=BC+BF=AC+CE=AE,
在Rt△CEF中,根据勾股定理得:CE2+CF2=EF2,
则AE2+BF2=EF2.
点评:此题考查了全等三角形的判定与性质,等腰直角三角形的性质,勾股定理,利用了等量代换的思想,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
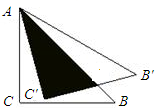 将直角边长为5cm的等腰直角△ABC绕点A逆时针旋转15°后,得到△AB′C′,则图中阴影部分的面积是( )cm2.
将直角边长为5cm的等腰直角△ABC绕点A逆时针旋转15°后,得到△AB′C′,则图中阴影部分的面积是( )cm2.| A、12.5 | ||||
B、
| ||||
C、
| ||||
| D、不能确定 |
 如图,AB为等腰直角△ABC的斜边(AB为定长线段),O为AB的中点,P为AC延长线上的一个动点,线段PB的垂直平分线交线段OC于点E,D为垂足,当P点运动时,给出下列四个结论,其中正确的个数是( )
如图,AB为等腰直角△ABC的斜边(AB为定长线段),O为AB的中点,P为AC延长线上的一个动点,线段PB的垂直平分线交线段OC于点E,D为垂足,当P点运动时,给出下列四个结论,其中正确的个数是( ) 如图,等腰直角△ABC中,∠ABC=90°,点D在AC上,将△ABD绕顶点B沿顺时针方向旋90°后得到△CBE.
如图,等腰直角△ABC中,∠ABC=90°,点D在AC上,将△ABD绕顶点B沿顺时针方向旋90°后得到△CBE.