题目内容
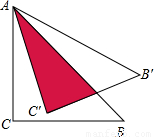
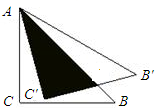 将直角边长为5cm的等腰直角△ABC绕点A逆时针旋转15°后,得到△AB′C′,则图中阴影部分的面积是( )cm2.
将直角边长为5cm的等腰直角△ABC绕点A逆时针旋转15°后,得到△AB′C′,则图中阴影部分的面积是( )cm2.| A、12.5 | ||||
B、
| ||||
C、
| ||||
| D、不能确定 |
分析:设AB与B′C′交于D点,根据旋转角∠CAC′=15°,等腰直角△ABC的一锐角∠CAB=45°,可求∠C′AD,旋转前后对应边相等,对应角相等,AC′=AC=5,∠C′=∠C=90°,解直角△AC′D,可求阴影部分面积.
解答: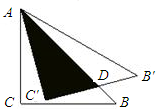 解:设AB与B′C′交于D点,
解:设AB与B′C′交于D点,
根据旋转性质得∠CAC′=15°,而∠CAB=45°,
∴∠C′AD=∠CAB-∠CAC′=30°,
又∵AC′=AC=5,∠C′=∠C=90°,
∴C′D=AC′•tan30°=
,
阴影部分面积为:
×5×
=
.故选B.
 解:设AB与B′C′交于D点,
解:设AB与B′C′交于D点,根据旋转性质得∠CAC′=15°,而∠CAB=45°,
∴∠C′AD=∠CAB-∠CAC′=30°,
又∵AC′=AC=5,∠C′=∠C=90°,
∴C′D=AC′•tan30°=
5
| ||
| 3 |
阴影部分面积为:
| 1 |
| 2 |
5
| ||
| 3 |
25
| ||
| 6 |
点评:本题考查了旋转的性质,等腰三角形的性质.关键是通过旋转的性质判断阴影部分三角形的特点,计算三角形的面积.

练习册系列答案
相关题目
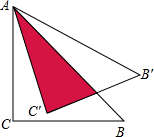 将直角边长为5cm的等腰直角△ABC绕点A逆时针旋转15°后,得到△AB′C′,则图中阴影部分的面积是
将直角边长为5cm的等腰直角△ABC绕点A逆时针旋转15°后,得到△AB′C′,则图中阴影部分的面积是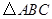 绕点
绕点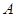 逆时针旋转
逆时针旋转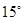 后得到
后得到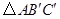 ,则图中阴影部分的面积是
,则图中阴影部分的面积是
 。
。