题目内容
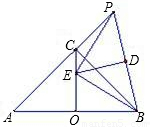
 如图,AB为等腰直角△ABC的斜边(AB为定长线段),O为AB的中点,P为AC延长线上的一个动点,线段PB的垂直平分线交线段OC于点E,D为垂足,当P点运动时,给出下列四个结论,其中正确的个数是( )
如图,AB为等腰直角△ABC的斜边(AB为定长线段),O为AB的中点,P为AC延长线上的一个动点,线段PB的垂直平分线交线段OC于点E,D为垂足,当P点运动时,给出下列四个结论,其中正确的个数是( )①E为△ABP的外心;②∠PEB=90°;③PC•BE=OE•PB;④
| 2 |
| ||
| 2 |
分析:①由于外心是三角形三边中垂线的交点,显然点E是AB、BP两边中垂线的交点,因此符合△ABP外心的要求,故①正确;
②此题要通过①的结论来求,连接AE,根据三角形的外心的性质可知:AE=PE=BE,即∠EPA=∠EAP,∠EAB=∠EBA,再结合三角形的内角和定理进行求解即可;
③此题显然要通过相似三角形来求解,由于OA=OB,那么可通过证△OEB∽△CPB来判断③的结论是否正确;
④此题较简单,过E作EM⊥OC,交AC于M,那么MC=
CE,因此所求的结论可转化为证PM是否为定值,观察图形,可通过证△PEM、△BEC是否全等来判断.
②此题要通过①的结论来求,连接AE,根据三角形的外心的性质可知:AE=PE=BE,即∠EPA=∠EAP,∠EAB=∠EBA,再结合三角形的内角和定理进行求解即可;
③此题显然要通过相似三角形来求解,由于OA=OB,那么可通过证△OEB∽△CPB来判断③的结论是否正确;
④此题较简单,过E作EM⊥OC,交AC于M,那么MC=
| 2 |
解答:解:①∵CO为等腰Rt△ABC斜边AB上的中线,
∴CO垂直平分AB;
又∵DE平分PB,即E点是AB、BP两边中垂线的交点,
∴E点是△ABP的外心,故①正确;
②如图,连接AE;
由①知:AE=EP=EB,则∠EAP=∠EPA,∠EPB=∠EBP,∠EAB=∠EBA;
∵∠PAB=45°,即∠EAP+∠EPA+∠EAB+∠EBA=2(∠EAP+∠EAB)=2∠PAB=90°,
由三角形内角和定理知:∠EPB+∠EBP=90°,即∠EPB=∠EBP=45°,
∴△PEB是等腰直角三角形;故②正确;
③∵∠PBE=∠ABC=45°,
∴∠EBO=∠PBC=45°-∠CBE,
又∵∠EOB=∠PCB=90°,
∴△BPC∽△BEO,得:
=
,即PC•BE=OE•PB,故③正确;
④过E作EM⊥OC,交AC于M;
易知:△EMC是等腰直角三角形,即MC=
EC,∠PME=45°;
∴∠PEM=∠BEC=90°+∠PEC,
又∵EC=ME,PE=BE,
∴△PME≌△BCE(SAS),得PM=BC=
AB,即PM是定值;
由于PM=CM+PC=
EC+PC,所以
CE+PC的值不变为
AB,故④正确;
因此正确的结论是①②③④,
故选D.
∴CO垂直平分AB;
又∵DE平分PB,即E点是AB、BP两边中垂线的交点,
∴E点是△ABP的外心,故①正确;
②如图,连接AE;
由①知:AE=EP=EB,则∠EAP=∠EPA,∠EPB=∠EBP,∠EAB=∠EBA;
∵∠PAB=45°,即∠EAP+∠EPA+∠EAB+∠EBA=2(∠EAP+∠EAB)=2∠PAB=90°,
由三角形内角和定理知:∠EPB+∠EBP=90°,即∠EPB=∠EBP=45°,
∴△PEB是等腰直角三角形;故②正确;
③∵∠PBE=∠ABC=45°,
∴∠EBO=∠PBC=45°-∠CBE,

又∵∠EOB=∠PCB=90°,
∴△BPC∽△BEO,得:
| PC |
| EO |
| BP |
| BE |
④过E作EM⊥OC,交AC于M;
易知:△EMC是等腰直角三角形,即MC=
| 2 |
∴∠PEM=∠BEC=90°+∠PEC,
又∵EC=ME,PE=BE,
∴△PME≌△BCE(SAS),得PM=BC=
| ||
| 2 |
由于PM=CM+PC=
| 2 |
| 2 |
| ||
| 2 |
因此正确的结论是①②③④,
故选D.
点评:本题考查了三角形外心的性质,线段中垂线性质,等腰直角三角形性质,三角形相似的判定,三角形全等的判定.此题为几何综合题,涉及较多的平面图形的性质,要求学生具备较强的分析问题、解决问题的能力,特别③、④两个结论的判别,有较大难度.此题可作为优秀学生的选拔.

练习册系列答案
相关题目
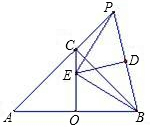 如图,AB为等腰直角△ABC的斜边(AB为定长线段),O为AB的中点,P为AC延长线上的一个动点,线段PB的垂直平分线交线段OC于点E,D为垂足,当P点运动时,给出下列四个结论:
如图,AB为等腰直角△ABC的斜边(AB为定长线段),O为AB的中点,P为AC延长线上的一个动点,线段PB的垂直平分线交线段OC于点E,D为垂足,当P点运动时,给出下列四个结论: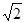 CE + PC的值不变.
CE + PC的值不变.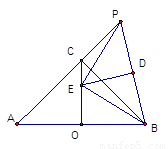
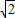 CE+PC的值不变.
CE+PC的值不变.
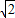 CE+PC的值不变.
CE+PC的值不变.