题目内容
13.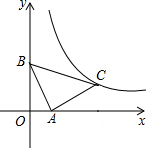 如图,在平面直角坐标系中,直线y=-2x+2与x轴、y轴分别交于A、B两点,△BAC为等腰直角三角形,且∠BAC=90°.若点C恰好落在函数y=$\frac{k}{x}$(x>0)在第一象限内的图象上,则k的值为( )
如图,在平面直角坐标系中,直线y=-2x+2与x轴、y轴分别交于A、B两点,△BAC为等腰直角三角形,且∠BAC=90°.若点C恰好落在函数y=$\frac{k}{x}$(x>0)在第一象限内的图象上,则k的值为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 直接过点C作CD⊥x轴于点D,得出△OAB≌△CDA(AAS),进而得出OD,CD的长,即可得出答案.
解答 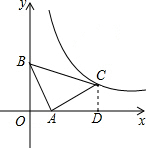 解:过点C作CD⊥x轴于点D,
解:过点C作CD⊥x轴于点D,
∵直线y=-2x+2与x轴、y轴分别交于A、B两点,
∴x=0时,y=2;y=0时,x=1,
则AO=1,OB=2,
∵△BAC为等腰直角三角形,且∠BAC=90°,
∴AB=AC,∠OAB+∠DAC=90°,
∵∠ACD+∠CAD=90°,
∴∠OAB=∠ACD,
在△OAB和△CDA中
$\left\{\begin{array}{l}{∠BOA=∠CDA}\\{∠OAB=∠ACD}\\{AB=AC}\end{array}\right.$,
∴△OAB≌△CDA(AAS),
∴AO=CD=1,OB=AD=2,
∴OD=3,CD=1,
∴k=3×1=3.
故选:C.
点评 此题主要考查了反比例函数图象上点的坐标性质以及全等三角形的判定与性质,正确得出OD,CD的长是解题关键.

练习册系列答案
相关题目
3.计算:$\frac{{{a^2}-1}}{{{{(a+1)}^2}}}$÷$\frac{a-1}{a}$,其结果正确的是( )
| A. | $\frac{1}{2}$ | B. | $\frac{a+1}{a+2}$ | C. | $\frac{a+1}{a}$ | D. | $\frac{a}{a+1}$ |
4.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
18.已知xa=3,xb=5,则xa-2b=( )
| A. | $\frac{3}{25}$ | B. | $\frac{3}{10}$ | C. | -22 | D. | -7 |
5.九年一班甲、乙、丙、丁四名同学几次数学测试成绩的平均数$\overline{x}$(分)及方差S2如下表:
老师想从中选派一名成绩较好且状态稳定的同学参加全省中学生数学竞赛,那么应选( )
| 甲 | 乙 | 丙 | 丁 | |
| 平均数(分) | 145 | 146 | 145 | 146 |
| 方差 | 1 | 1 | 1.5 | 1.7 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
 如图在△ABC中,AD⊥BC,垂足为D,E是AC边上一点,BE与AD交于点F,若∠ABC=45°,∠BAC=75°,∠BFD=60°.求∠BEC的度数.
如图在△ABC中,AD⊥BC,垂足为D,E是AC边上一点,BE与AD交于点F,若∠ABC=45°,∠BAC=75°,∠BFD=60°.求∠BEC的度数.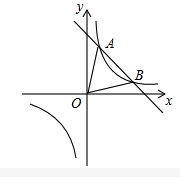 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(1,6),B(3,n)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(1,6),B(3,n)两点.