题目内容
12.已知A(3,2),B(3,-4),将线段AB向左平移8个单位长度得到线段CD.(1)写出C、D的坐标并画出图形;
(2)现将四边形ABCD以每秒0.5个单位长度的速度向x轴正方向平移,多长时间后△OCD的面积是四边形ABCD的面积的$\frac{1}{4}$?
(3)现将四边形ABCD以每秒0.5个单位长度的速度向y轴正方向平移,多长时间后△OBD的面积是四边形ABCD的面积的$\frac{1}{4}$?
分析 (1)根据题意画出图形,根据C、D两点在坐标系中的位置写出C、D两点的坐标即可;
(2)先求出四边形ABCD的面积,再由△OCD的面积是四边形ABCD的面积的$\frac{1}{4}$可得出△OCD的高,进而可得出结论;
(3)先求出BD的长,再求出其高即可得出结论.
解答  解:(1)如图所示,C(-5,2),D(-5,-4);
解:(1)如图所示,C(-5,2),D(-5,-4);
(2)∵S四边形ABCD=6×8=48,
∴S△OCD=$\frac{1}{4}$×6×8=12.
∵CD=6,
∴△OCD的高=$\frac{12}{3}$=4,
∴四边形ABCD向右平移1个单位或8个单位时,△OCD的面积是四边形ABCD的面积的$\frac{1}{4}$.
∵四边形ABCD以每秒0.5个单位长度的速度向x轴正方向平移,
∴t=$\frac{1}{0.5}$=2(秒)或t=$\frac{9}{0.5}$=18(秒).
(3)∵由(1)知四边形ABCD的面积是48,
∴△OBD的面积是12.
∵BD=8,
∴△OCD的高=$\frac{12×2}{8}$=3,
∴四边形ABCD向上平移1个单位或7个单位时,△OBD的面积是四边形ABCD的面积的$\frac{1}{4}$,
∴t=$\frac{1}{0.5}$=2(秒)或t=$\frac{7}{0.5}$=15(秒).
点评 本题考查的是作图-平移变换,根据图形平移的性质画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
7.一辆汽车从A地出发,向东行驶,途中要经过十字路口B,在规定的某一段时间内,若车速为每小时60千米,就能驶过B处2千米;若每小时行驶50千米,就差3千米才能到达B处,设A、B间的距离为x千米,规定的时间为y小时,则可列出方程组是( )
| A. | $\left\{\begin{array}{l}{60y-x=2}\\{x=3-50y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{60y-x=2}\\{50y-x=3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{60y=x+2}\\{50y=x-3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{60y=x-2}\\{50y=x+3}\end{array}\right.$ |
 如图,若∠1=∠2,∠C=∠D.∠A和∠F是什么关系?为什么?
如图,若∠1=∠2,∠C=∠D.∠A和∠F是什么关系?为什么?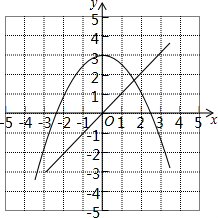 我们在求方程x2+2x-6=0的近似根时,可以将原方程变形为-$\frac{1}{2}$x2+3=x,然后在同一直角坐标系中画出函数y=-$\frac{1}{2}$x2+3和y=x的图象,发现-4<x1<-3,1<x2<2.请你利用已有的函数图象判断方程x3-6x+12=0在实数范围内有几个解?
我们在求方程x2+2x-6=0的近似根时,可以将原方程变形为-$\frac{1}{2}$x2+3=x,然后在同一直角坐标系中画出函数y=-$\frac{1}{2}$x2+3和y=x的图象,发现-4<x1<-3,1<x2<2.请你利用已有的函数图象判断方程x3-6x+12=0在实数范围内有几个解?