题目内容
12. 某蔬菜基地的圆弧形大棚的剖面如图所示,已知中间柱CD=2m,AB=8m,则半径OA的长为5m.
某蔬菜基地的圆弧形大棚的剖面如图所示,已知中间柱CD=2m,AB=8m,则半径OA的长为5m.
分析 根据垂径定理可得AD=$\frac{1}{2}$AB=4m,设AO=xm,则DO=(x-2)m,根据勾股定理可得(x-2)2+42=x2,再解方程即可.
解答 解:∵CO⊥AB,
∴AD=$\frac{1}{2}$AB=4m,
设AO=xm,则DO=(x-2)m,
(x-2)2+42=x2,
解得:x=5.
故答案为:5.
点评 此题主要考查了垂径定理的应用,以及勾股定理的应用,关键是掌握平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.

练习册系列答案
相关题目
3.点(1,m),(2,n)在函数y=-x+1的图象上,则m、n的大小关系是( )
| A. | m>n | B. | m<n | C. | m=n | D. | m≤n |
7.若⊙O1、⊙O2的半径分别为2和5,圆心距O1O2=6,则⊙O1与⊙O2的位置关系是( )
| A. | 内切 | B. | 相交 | C. | 外切 | D. | 外离 |
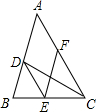 如图,CD是△ABC的角平分线,点E、F分别在BC、AC上,且DE∥AC,FE∥AB.
如图,CD是△ABC的角平分线,点E、F分别在BC、AC上,且DE∥AC,FE∥AB.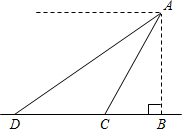 如图,从山顶A处看地面D点的俯角为30°,看地面C点的俯角为60°,测得CD=200米,求山高AB.(精确到0.1米,$\sqrt{3}$≈1.732)
如图,从山顶A处看地面D点的俯角为30°,看地面C点的俯角为60°,测得CD=200米,求山高AB.(精确到0.1米,$\sqrt{3}$≈1.732)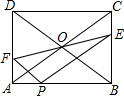 如图,矩形ABCD中,对角线AC,BD相交于点O,AB=4,BC=3,在线段AB上取一点P,过点P作AC的平行线交BC于点E,连结EO并延长交AD于点F,连接PF.
如图,矩形ABCD中,对角线AC,BD相交于点O,AB=4,BC=3,在线段AB上取一点P,过点P作AC的平行线交BC于点E,连结EO并延长交AD于点F,连接PF.