题目内容
17.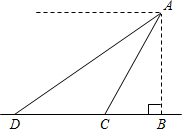 如图,从山顶A处看地面D点的俯角为30°,看地面C点的俯角为60°,测得CD=200米,求山高AB.(精确到0.1米,$\sqrt{3}$≈1.732)
如图,从山顶A处看地面D点的俯角为30°,看地面C点的俯角为60°,测得CD=200米,求山高AB.(精确到0.1米,$\sqrt{3}$≈1.732)
分析 设山高AB的高度为x米,在Rt△ABD中,∠ADB=30°,利用三角函数可以用x表示BD的长度,在Rt△ABC中,∠ACB=60°,可以得到BC=x,而CD=DB-BC,由此根据已知条件可以得到关于x的方程,解方程即可求解.
解答 解:由题意可知:∠ADB=30°,∠ACB=60°,设山高AB为x米
∵在Rt△ABC中,tan∠ACB=$\frac{AB}{DB}$,
∴CB=$\frac{AB}{tan∠ACB}$=$\frac{x}{tan60°}$=$\frac{x}{\sqrt{3}}$,
∵在Rt△ABD中,tan∠ADB=$\frac{AB}{DB}$,
∴DB=$\frac{AB}{tan∠ADB}$=$\frac{x}{tan30°}$=$\sqrt{3}$x,
∵BD-CB=CD
∴$\sqrt{3}$x-$\frac{x}{\sqrt{3}}$=200,
∴x=100$\sqrt{3}$≈173.2.
答:山高AB约173.2米.
点评 此题主要考查了解直角三角形-仰角、俯角的问题,解题的关键是正确理解仰角、俯角的定义,然后利用三角函数可以列出关于x的方程解决问题.

练习册系列答案
相关题目
5.下列运算正确的是( )
| A. | a4•a2=a8 | B. | a4+a2=a6 | C. | a2÷a-1=a3 | D. | (-2a3)2=-4a6 |
9.在数据分析的过程中,有人对两个不同城市学生的数学成绩进行了分析,结果发现这两座城市统计的方差值都是10.34,那么下列说法中,正确的是( )
| A. | 两城市学生的成绩一样 | B. | 两城市学生的数学平均分一样 | ||
| C. | 两城市数学成绩的中位数一样 | D. | 两城市学生数学成绩波动情况一样 |
 某蔬菜基地的圆弧形大棚的剖面如图所示,已知中间柱CD=2m,AB=8m,则半径OA的长为5m.
某蔬菜基地的圆弧形大棚的剖面如图所示,已知中间柱CD=2m,AB=8m,则半径OA的长为5m.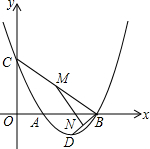 已知二次函数y=x2+bx+c,其图象交x轴于点A(1,0),B(3,0),交y轴于点C,点D为顶点.
已知二次函数y=x2+bx+c,其图象交x轴于点A(1,0),B(3,0),交y轴于点C,点D为顶点.