题目内容
4.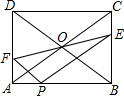 如图,矩形ABCD中,对角线AC,BD相交于点O,AB=4,BC=3,在线段AB上取一点P,过点P作AC的平行线交BC于点E,连结EO并延长交AD于点F,连接PF.
如图,矩形ABCD中,对角线AC,BD相交于点O,AB=4,BC=3,在线段AB上取一点P,过点P作AC的平行线交BC于点E,连结EO并延长交AD于点F,连接PF.(1)求证:PF∥BD;
(2)设AP的长为x,△PEF的面积为y,求y与x的函数关系式,并写出它的定义域.
分析 (1)根据矩形的性质求得AD∥BC,OA=OC,AD=BC,然后通过ASA证得△AOF≌△COE,得出AF=CE,DF=BE,然后通过平行线分线段长比例定理求得$\frac{PB}{PA}$=$\frac{BE}{CE}$=$\frac{DF}{AF}$,即可证得PF∥BD.
(2)根据S△PEF=S梯形ABEF-S△APF-S△PBE即可求得.
解答 解:(1)∵四边形ABCD是矩形,
∴AD∥BC,OA=OC,AD=BC,
∴∠OAF=∠OCE,
在△AOF和△COE中,
$\left\{\begin{array}{l}{∠OAF=∠OCE}\\{OA=OC}\\{∠AOF=∠COE}\end{array}\right.$,
∴△AOF≌△COE(ASA),
∴AF=CE,
∴DF=BE,
∵PE∥AC,
∴△PBE∽△ABC,
∴$\frac{PB}{PA}$=$\frac{BE}{CE}$,
∴$\frac{PB}{PA}$=$\frac{DF}{AF}$,
∴PF∥BD.
(2)∵PF∥BD,
∴$\frac{PA}{AB}$=$\frac{FA}{AD}$,
∵AB=4,BC=3,AP的长为x,
∴$\frac{x}{4}$=$\frac{FA}{3}$,
∴FA=$\frac{3}{4}$x,
∵FA=CE,
∴BE=4-CE=3-$\frac{3}{4}$x,
∴S△PEF=S梯形ABEF-S△APF-S△PBE=$\frac{1}{2}$(AF+BE)•AB-$\frac{1}{2}$AF•AP-$\frac{1}{2}$PB•PE,
即y=$\frac{1}{2}$×3×4-$\frac{1}{2}$×$\frac{3}{4}$x•x-$\frac{1}{2}$(4-x)(3-$\frac{3}{4}$x)=-$\frac{3}{4}$x2+3x,
∴y=-$\frac{3}{4}$x2+3x.(0<x<4).
点评 本题考查了矩形的性质,平行线分线段成比例定理,梯形的面积以及三角形的面积等,熟练掌握性质定理是解题的关键.

 全能测控一本好卷系列答案
全能测控一本好卷系列答案| A. | 1-$\sqrt{2}$ | B. | 1+$\sqrt{2}$ | C. | -$\sqrt{2}$ | D. | $\sqrt{2}$ |
| A. | 两城市学生的成绩一样 | B. | 两城市学生的数学平均分一样 | ||
| C. | 两城市数学成绩的中位数一样 | D. | 两城市学生数学成绩波动情况一样 |
| A. | $\frac{a}{a-1}$ | B. | $\frac{a+1}{a-1}$ | C. | $\frac{a}{a+1}$ | D. | a |
| A. | a-4>b-4 | B. | -$\frac{a}{3}$<-$\frac{b}{3}$ | C. | -2a<-2b | D. | -5+a<-5+b |
 某蔬菜基地的圆弧形大棚的剖面如图所示,已知中间柱CD=2m,AB=8m,则半径OA的长为5m.
某蔬菜基地的圆弧形大棚的剖面如图所示,已知中间柱CD=2m,AB=8m,则半径OA的长为5m.