题目内容
16.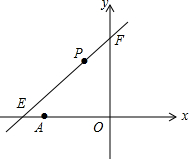 如图,直线l:y=kx+6与x轴、y轴分别相交于E、F,点E的坐标为(-9,0),点A的坐标为(-6,0),点P(x,y)是直线l上的一个动点.
如图,直线l:y=kx+6与x轴、y轴分别相交于E、F,点E的坐标为(-9,0),点A的坐标为(-6,0),点P(x,y)是直线l上的一个动点.(1)求出△OPA的面积S与x的函数关系式.
(2)当△OPA的面积为3.6时,求点P的坐标.
(3)若直线OP分△OEF的面积为1:2两部分时,求点P的坐标.
分析 (1)思想求出直线EF的解析式,则P(x,$\frac{2}{3}$x+6),根据三角形的面积公式,利用分段函数表示S即可;
(2)利用(1)中结论,列出方程,解方程即可;
(3)由S△EOF=$\frac{1}{2}$×9×6=27,直线OP分△OEF的面积为1:2两部分,可得S△PEO=9或18,可得$\frac{1}{2}$×9×($\frac{2}{3}$x+6)=9或$\frac{1}{2}$×9×($\frac{2}{3}$x+6)=18,解方程即可解决问题;
解答 解:(1)∵直线y=kx+6经过点E(-9,0),
∴-9k+6=0,
∴k=$\frac{2}{3}$,
∴y=$\frac{2}{3}$x+6,
∴P(x,$\frac{2}{3}$x+6),
∴S=$\frac{1}{2}$•OA•|$\frac{2}{3}$x+6|=$\left\{\begin{array}{l}{2x+18}&{(x≥-9)}\\{-2x-18}&{(x<-9)}\end{array}\right.$.
(2)由题意2x+18=3.6或-2x-18=3.6,
解得x=-7.2或x=-10.8,
∴当△OPA的面积为3.6时,点P的坐标为(-7.2,1.2)或(-10.8,-1.2).
(3)∵S△EOF=$\frac{1}{2}$×9×6=27,直线OP分△OEF的面积为1:2两部分,
∴S△PEO=9或18,
∴$\frac{1}{2}$×9×($\frac{2}{3}$x+6)=9或$\frac{1}{2}$×9×($\frac{2}{3}$x+6)=18,
解得x=-6或-3,
此时点P坐标为(-6,2)或(-3,4).
点评 本题考查三角形综合题、一次函数图象上点的坐标特点、三角形的面积公式等知识,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键,学会用构建方程的思想思考问题,把问题转化为方程解决,属于中考压轴题.

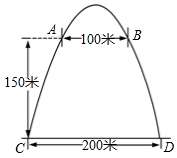 如图,拱门的地面宽度为200米,两侧距地面高150米处各有一个观光窗,两窗的水平距离为100米,则拱门的最大高度( )
如图,拱门的地面宽度为200米,两侧距地面高150米处各有一个观光窗,两窗的水平距离为100米,则拱门的最大高度( )| A. | 100米 | B. | 150米 | C. | 200米 | D. | 300米 |
 星期天早上,淇淇从家跑步到公园,接着马上原路步行回家,如图所示的是淇淇离家的路程y(米)与时间t(分)的函数图象,则淇淇回家的速度是每分钟步行90米.
星期天早上,淇淇从家跑步到公园,接着马上原路步行回家,如图所示的是淇淇离家的路程y(米)与时间t(分)的函数图象,则淇淇回家的速度是每分钟步行90米.