题目内容
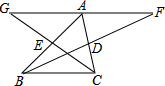如图，在△ABC中，BD、CE分别是AC、AB边上的中线，分别延长BD、CE到F、G，使DF=BD，EG=CE，则下列结论：①GA=AF，②GA∥BC，③AF∥BC，④G、A、F在一条直线上，⑤A是线段GF的中点，其中正确的有（ ）| A、5个 | B、4个 | C、3个 | D、2个 |
考点：全等三角形的判定与性质
专题：
分析：易证△AEG≌△BEC，△ADF≌△CDB，根据全等三角形对应角、对应边相等的性质，对题干中给出5个结论分别验证，即可解题．
解答：解：在△AEG和△BEC中，
，
∴△AEG≌△BEC，（SAS）
∴BC=AG，∠BCE=∠G，
∴AG∥BC，②正确；
在△AEG和△BEC中，
，
∴△AEG≌△BEC，（SAS）
∴BC=AF，∠DBC=∠F，
∴AF∥BC，③正确；
∴AF=AG，①正确；
∴A是线段GF的中点，⑤正确；
∵AF，AG都经过点A，
∴G、A、F在一条直线上，④正确；
故选：A．
|
∴△AEG≌△BEC，（SAS）
∴BC=AG，∠BCE=∠G，
∴AG∥BC，②正确；
在△AEG和△BEC中，
|
∴△AEG≌△BEC，（SAS）
∴BC=AF，∠DBC=∠F，
∴AF∥BC，③正确；
∴AF=AG，①正确；
∴A是线段GF的中点，⑤正确；
∵AF，AG都经过点A，
∴G、A、F在一条直线上，④正确；
故选：A．
点评：本题考查了全等三角形的判定，考查了全等三角形对应角、对应边相等的性质，本题中求证△AEG≌△BEC和△AEG≌△BEC是解题的关键．
练习册系列答案
相关题目
若a＞0，b＞0，则下列各式中正确的是（ ）
| A、a-b＞0 |
| B、a-b＜0 |
| C、a-b=0 |
| D、-a-b＜0 |
如图，一张矩形纸片ABCD，按图示加以折叠，使得顶点C落在AB边上的E处，若AD=6，则折痕DF的长为（ ）| A、7 | ||
B、7
| ||
| C、8 | ||
D、8
|
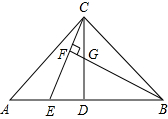已知：在△ABC中，AC=BC，∠ACB=90°，CD⊥AB，点E是AB边上一点．直线BF⊥CE于点F，交CD于点G（如图），求证：
一座圆弧形拱桥如图，圆弧形桥拱的跨度AB=12米，C为桥拱的中点，拱高CD=4米，求拱桥的半径．
已知一次函数y=-kx+k的图象如图，则二次函数y=-kx2-2x+k的图象大致是（ ）
