题目内容
已知正九边形的边长为a,则这个正九边形的外接圆的半径为 .
考点:正多边形和圆
专题:
分析:如图,求出∠AOC的度数,AC的长度,运用直角三角形的边角关系即可解决问题.
解答: 解:如图,设AB为正九边形的一边,OC为边心距;
解:如图,设AB为正九边形的一边,OC为边心距;
∵OA=OB,OC⊥AB,
∴∠AOC=∠BOC=
∠AOB;AC=BC=
a;
∵∠AOB=
=40°,
∴∠AOC=20°;
∵sin∠AOC=
,
∴OA=
,
故答案为:
.
 解:如图,设AB为正九边形的一边,OC为边心距;
解:如图,设AB为正九边形的一边,OC为边心距;∵OA=OB,OC⊥AB,
∴∠AOC=∠BOC=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠AOB=
| 360° |
| 9 |
∴∠AOC=20°;
∵sin∠AOC=
| AC |
| OA |
∴OA=
| a |
| 2sin20° |
故答案为:
| a |
| 2sin20° |
点评:该题主要考查了正多边形和圆的性质及其应用问题;解题的关键是大胆猜测、合情推理、科学论证.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
参加一次聚会的每两人都握了一次手,所有人握手10次,则参加聚会的人共有( )人.
| A、4 | B、5 | C、6 | D、7 |
 如图,BD垂直平分AC,则结论①AB=AD;②AD=DC;③∠BAC=∠DAC;④∠ABD=∠CBD中成立的是
如图,BD垂直平分AC,则结论①AB=AD;②AD=DC;③∠BAC=∠DAC;④∠ABD=∠CBD中成立的是 如图,在△ABC中,∠ACB=90°,AD⊥AB,AD=AB,BE⊥DC,AF⊥AC,求证:CF平分∠ACB.
如图,在△ABC中,∠ACB=90°,AD⊥AB,AD=AB,BE⊥DC,AF⊥AC,求证:CF平分∠ACB.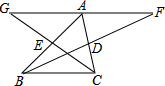 如图,在△ABC中,BD、CE分别是AC、AB边上的中线,分别延长BD、CE到F、G,使DF=BD,EG=CE,则下列结论:①GA=AF,②GA∥BC,③AF∥BC,④G、A、F在一条直线上,⑤A是线段GF的中点,其中正确的有( )
如图,在△ABC中,BD、CE分别是AC、AB边上的中线,分别延长BD、CE到F、G,使DF=BD,EG=CE,则下列结论:①GA=AF,②GA∥BC,③AF∥BC,④G、A、F在一条直线上,⑤A是线段GF的中点,其中正确的有( ) 某旅游观光车在距指挥中心90km的草原上出现故障,指挥中心得到消息后派出巡逻车前往接应,同时游客们沿着指挥中心的方向步行.巡逻车接走第一批游客到达指挥中心后,立即原速原路返回接应第二批游客,第二批游客在此期间继续原速步行.如图为游客与巡逻车距出事地点的路程y(km)和时间x(h)之间的函数图象.求巡逻车与第二批游客相遇时的距指挥中心的路程及时间.
某旅游观光车在距指挥中心90km的草原上出现故障,指挥中心得到消息后派出巡逻车前往接应,同时游客们沿着指挥中心的方向步行.巡逻车接走第一批游客到达指挥中心后,立即原速原路返回接应第二批游客,第二批游客在此期间继续原速步行.如图为游客与巡逻车距出事地点的路程y(km)和时间x(h)之间的函数图象.求巡逻车与第二批游客相遇时的距指挥中心的路程及时间.