题目内容
某超市欲购进AB 两种竹盐100箱(每箱40袋),两种竹盐的相关信息如下表:
根据上述信息,该店巨鼎用更超过5020元,但不超过5120元的资金购进这两种竹盐.
(1)该超市有哪几种进货方案;
(2)该超市按哪种进货方案所获得的利润最大,最大利润是多少?
(3)市民抢购竹盐,在(2)的条件下进货后,该超市决定将购进的这两种竹盐的价格均上调后再出售(上调是进价的整数倍),开始销售时及被抢购一空,超市获得的利润为10240元,请直接写出上调价格后两种竹盐每袋的销售价格.
| 竹盐 | A | B |
| 进价(元/箱) | 32 | 80 |
| 售价(元/箱) | 48 | 100 |
(1)该超市有哪几种进货方案;
(2)该超市按哪种进货方案所获得的利润最大,最大利润是多少?
(3)市民抢购竹盐,在(2)的条件下进货后,该超市决定将购进的这两种竹盐的价格均上调后再出售(上调是进价的整数倍),开始销售时及被抢购一空,超市获得的利润为10240元,请直接写出上调价格后两种竹盐每袋的销售价格.
考点:一次函数的应用,一元一次不等式组的应用
专题:
分析:(1)设购进A种竹盐x箱,则购进B种竹盐(100-x)箱,根据两种竹盐的总价超过5020元,但不超过5120元建立不等式组求出其解即可;
(2)设竹盐的总利润为W元,由利润=(售价-进件)×数量,就可以得出W与x的关系式,由一次函数的解析式的性质就可以得出结论;
(3)设A种竹盐上调了a倍,B种竹盐上调了b倍,由总利润=两种竹盐的利润之和建立方程求出其解即可.
(2)设竹盐的总利润为W元,由利润=(售价-进件)×数量,就可以得出W与x的关系式,由一次函数的解析式的性质就可以得出结论;
(3)设A种竹盐上调了a倍,B种竹盐上调了b倍,由总利润=两种竹盐的利润之和建立方程求出其解即可.
解答:解:(1)设购进A种竹盐x箱,则购进B种竹盐(100-x)箱,由题意,得,
5020<32x+80(100-x)≤5120,
解得:60≤x<62
,
∵x为整数,
∴x=60,61,62.
∴有三种进货方案.
方案1,购进A种竹60箱,购进B种竹盐40箱,
方案2,购进A种竹61箱,购进B种竹盐39箱,
方案3,购进A种竹62箱,购进B种竹盐38箱,
(2)设竹盐的总利润为W元,由题意,得
W=(48-32)x+(100-80)(100-x),
=-4x+2000.
∴k=-4<0,
∴W随x的增大而减小,
∴当x=60时,W最大=1760元.
(3)设A种竹盐上调了a倍,B种竹盐上调了b倍,由题意,得
60×32a+40×80b=10240,
∴a=
.
∵a为正整数,
∴
>0,
∴b<
.
∴b=1,2,3
∵a为正整数,
∴b=2时,a=2.
∴A种竹盐每箱的售价为:32×(1+2)=96元,B种竹盐每箱售价为:80×(1+2)=240
∴A种竹盐每袋的售价为:96÷40=2.4元,B种竹盐每袋售价为:240÷40=6元.
答:上调价格后A种竹盐每袋的销售价格为2.4元,B种竹盐每袋的销售价格为6元.
5020<32x+80(100-x)≤5120,
解得:60≤x<62
| 1 |
| 12 |
∵x为整数,
∴x=60,61,62.
∴有三种进货方案.
方案1,购进A种竹60箱,购进B种竹盐40箱,
方案2,购进A种竹61箱,购进B种竹盐39箱,
方案3,购进A种竹62箱,购进B种竹盐38箱,
(2)设竹盐的总利润为W元,由题意,得
W=(48-32)x+(100-80)(100-x),
=-4x+2000.
∴k=-4<0,
∴W随x的增大而减小,
∴当x=60时,W最大=1760元.
(3)设A种竹盐上调了a倍,B种竹盐上调了b倍,由题意,得
60×32a+40×80b=10240,
∴a=
| 16-5b |
| 3 |
∵a为正整数,
∴
| 16-5b |
| 3 |
∴b<
| 16 |
| 5 |
∴b=1,2,3
∵a为正整数,
∴b=2时,a=2.
∴A种竹盐每箱的售价为:32×(1+2)=96元,B种竹盐每箱售价为:80×(1+2)=240
∴A种竹盐每袋的售价为:96÷40=2.4元,B种竹盐每袋售价为:240÷40=6元.
答:上调价格后A种竹盐每袋的销售价格为2.4元,B种竹盐每袋的销售价格为6元.
点评:本题考查了列一元一次不等式组解实际问题的运用,一元一次不等式组的解法的运用,方案设计的运用,一次函数的性质的运用,二元一次不定方程的解法的运用,解答时求出函数的解析式是关键.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
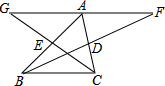 如图,在△ABC中,BD、CE分别是AC、AB边上的中线,分别延长BD、CE到F、G,使DF=BD,EG=CE,则下列结论:①GA=AF,②GA∥BC,③AF∥BC,④G、A、F在一条直线上,⑤A是线段GF的中点,其中正确的有( )
如图,在△ABC中,BD、CE分别是AC、AB边上的中线,分别延长BD、CE到F、G,使DF=BD,EG=CE,则下列结论:①GA=AF,②GA∥BC,③AF∥BC,④G、A、F在一条直线上,⑤A是线段GF的中点,其中正确的有( )| A、5个 | B、4个 | C、3个 | D、2个 |
 如图,⊙O的两条直径AB、CD互相垂直,弦MN垂直平分OB,交OB于点E,求证:MB与MC分别为该圆的内接正六边形和正十二边形的边长.
如图,⊙O的两条直径AB、CD互相垂直,弦MN垂直平分OB,交OB于点E,求证:MB与MC分别为该圆的内接正六边形和正十二边形的边长.
 二次函数y=ax2+bx+c图象如图,下列正确的个数为( )
二次函数y=ax2+bx+c图象如图,下列正确的个数为( )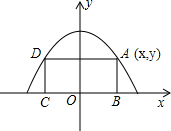 如图,矩形ABCD的顶点B,C在x轴上,A,D在抛物线y=-
如图,矩形ABCD的顶点B,C在x轴上,A,D在抛物线y=-