题目内容
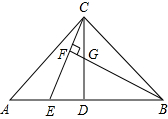 已知:在△ABC中,AC=BC,∠ACB=90°,CD⊥AB,点E是AB边上一点.直线BF⊥CE于点F,交CD于点G(如图),求证:
已知:在△ABC中,AC=BC,∠ACB=90°,CD⊥AB,点E是AB边上一点.直线BF⊥CE于点F,交CD于点G(如图),求证:(1)∠CGB=∠AEC;
(2)AE=CG.
考点:全等三角形的判定与性质
专题:证明题
分析:(1)易证∠CBG=∠ACE,根据三角形内角和为180°的性质可以求得∠CGB=∠AEC;
(2)根据(1)中结论易证△CGB≌△AEC,即可求得AE=CG.
(2)根据(1)中结论易证△CGB≌△AEC,即可求得AE=CG.
解答:解:(1)∵∠ACB=90°,CD⊥AB,
∴∠A=∠BCG=45°,
∵∠ACE+∠BCF=90°,∠BCF+∠CBF=90°,
∴∠CBG=∠ACE,
∵∠AEC=180°-∠A-∠ACE,∠CGB=180°-∠CBG-∠BCG,
∴∠AEC=∠CGB;
(2)在△BCG和△CAE中,
,
∴△BCG≌△CAE(ASA),
∴AE=CG.
∴∠A=∠BCG=45°,
∵∠ACE+∠BCF=90°,∠BCF+∠CBF=90°,
∴∠CBG=∠ACE,
∵∠AEC=180°-∠A-∠ACE,∠CGB=180°-∠CBG-∠BCG,
∴∠AEC=∠CGB;
(2)在△BCG和△CAE中,
|
∴△BCG≌△CAE(ASA),
∴AE=CG.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△BCG≌△CAE是解题的关键.

练习册系列答案
相关题目
作已知角的平分线是根据三角形的全等判定( )作的.
| A、AAS | B、ASA |
| C、SAS | D、SSS |
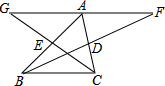 如图,在△ABC中,BD、CE分别是AC、AB边上的中线,分别延长BD、CE到F、G,使DF=BD,EG=CE,则下列结论:①GA=AF,②GA∥BC,③AF∥BC,④G、A、F在一条直线上,⑤A是线段GF的中点,其中正确的有( )
如图,在△ABC中,BD、CE分别是AC、AB边上的中线,分别延长BD、CE到F、G,使DF=BD,EG=CE,则下列结论:①GA=AF,②GA∥BC,③AF∥BC,④G、A、F在一条直线上,⑤A是线段GF的中点,其中正确的有( )| A、5个 | B、4个 | C、3个 | D、2个 |

 如图,AB为⊙O的直径,且AB⊥CD于点E,CD=16,AE=4,求DE的长.
如图,AB为⊙O的直径,且AB⊥CD于点E,CD=16,AE=4,求DE的长. 如图,⊙O的两条直径AB、CD互相垂直,弦MN垂直平分OB,交OB于点E,求证:MB与MC分别为该圆的内接正六边形和正十二边形的边长.
如图,⊙O的两条直径AB、CD互相垂直,弦MN垂直平分OB,交OB于点E,求证:MB与MC分别为该圆的内接正六边形和正十二边形的边长. 二次函数y=ax2+bx+c图象如图,下列正确的个数为( )
二次函数y=ax2+bx+c图象如图,下列正确的个数为( ) 如图,已知△ABC,用直尺和圆规画出一条线段a,使a=AC+BC,然后比较a与AB的长短.
如图,已知△ABC,用直尺和圆规画出一条线段a,使a=AC+BC,然后比较a与AB的长短.