题目内容
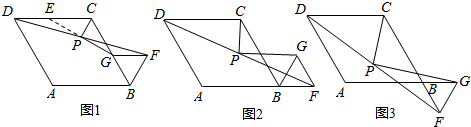
9.在菱形ABCD和正三角形BGF中,∠ABC=60°,P是DF的中点,连接PG、PC.(1)如图1,当点G在BC边上时,猜想PG与PC的关系,并证明.(提示:延长GP交CD于点E)
(2)如图2,当点F在AB的延长线上时,线段PC、PG还满足(1)中的结论吗?写出你的猜想,并给与证明;
(3)如图3,当点F在CB的延长线上时,线段PC、PG又有怎样的关系,直接写出你猜想.
分析 (1)延长GP交DC于点E,利用△PED≌△PGF,得出PE=PG,DE=FG,得到CE=CG,CP是EG的中垂线,在Rt△CPG中,∠PCG=60°,即可得出PG=$\sqrt{3}$PC.
(2)延长GP交DA于点E,连接EC,GC,先证明△DPE≌△FPG,再证得△CDE≌△CBG,利用在Rt△CPG中,∠PCG=60°,即可得出PG=$\sqrt{3}$PC.
(3)延长GP到H,使PH=PG,连接CH、DH,作FE∥DC,先证△GFP≌△HDP,再证得△HDC≌△GBC,在Rt△CPG中,∠PCG=60°,即可得出PG=$\sqrt{3}$PC.
解答 证明:(1)PC⊥PG且PG=$\sqrt{3}$PC,
如图1:延长GP交DC于点E,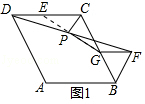
∵点P是DF的中点,
∴DP=FP,
∵△BGF是正三角形,
∴∠FGB=60°,
∴∠CGF=180°-60°=120°,
又∵菱形ABCD中,∠ABC=60°,
∴∠DCG=120°,
∴DC∥GF,
∴∠PDE=∠PFG,
在△PED和△PGF中,
$\left\{\begin{array}{l}{∠EPD=∠GPF}\\{DP=FP}\\{∠PDE=∠PFG}\end{array}\right.$
∴△PED≌△PGF(ASA),
∴PE=PG,DE=FG,
∵DC=BC,
∴CE=CG,
∴CP是EG的中垂线,即PC⊥PG
在RT△CPG中,∠PCG=60°,
∴PG=$\sqrt{3}$PC.
(2)猜想:CP⊥PG 且PG=$\sqrt{3}$PC.
如图2,延长GP交DA于点E,连接EC,GC,
∵∠ABC=60°,△BGF是正三角形,
∴∠BFG=60°,
∴GF∥BC∥AD,
∴∠EDP=∠GFP,
在△DPE和△FPG中
$\left\{\begin{array}{l}{∠EDP=∠GFP}\\{DP=FP}\\{∠DPE=∠FPG}\end{array}\right.$
∴△DPE≌△FPG(ASA)
∴PE=PG,DE=FG=BG,
∵∠CDE=CBG=60°,CD=CB,
在△CDE和△CBG中,
$\left\{\begin{array}{l}{CD=CB}\\{∠CDE=∠CBG=60°}\\{CD=CB}\end{array}\right.$
∴△CDE≌△CBG(SAS)
∴CE=CG,∠DCE=∠BCG,
∴∠ECG=∠DCB=120°,
∵PE=PG,
∴PC⊥PG,∠PCG=$\frac{1}{2}$∠ECG=60°
∴PG=$\sqrt{3}$PC;
(3)猜想:PG=$\sqrt{3}$PC,PG⊥PC.
如图3,延长GP到H,使PH=PG,连接CH,CG,DH,作FE∥DC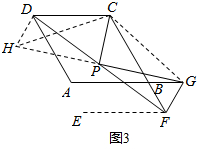
∵P是线段DF的中点,
∴FP=DP,
在△GFP和△HDP中,
$\left\{\begin{array}{l}{FP=DP}\\{∠GPF=∠HPD}\\{GP=HP}\end{array}\right.$
∴△GFP≌△HDP(SAS),
∴GF=HD,∠GFP=∠HDP,
∵∠GFP+∠PFE=120°,∠PFE=∠PDC,
∴∠CDH=∠HDP+∠PDC=120°,
∵四边形ABCD是菱形,
∴CD=CB,∠ADC=∠ABC=60°,点A、B、G又在一条直线上,
∴∠GBC=120°,
∵△BFG是等边三角形,
∴GF=GB,
∴HD=GB,
在△HDC和△GBC中,
$\left\{\begin{array}{l}{HD=GB}\\{∠HDC=∠GBC}\\{DC=BC}\end{array}\right.$
∴△HDC≌△GBC(SAS),
∴CH=CG,∠DCH=∠BCG,
∴∠DCH+∠HCB=∠BCG+∠HCB=120°,
即∠HCG=120°
∵CH=CG,PH=PG,
∴PG⊥PC,∠GCP=∠HCP=60°,
∴PG=$\sqrt{3}$PC.
点评 本题主要考查了菱形的性质,以及全等三角形的判定与性质等知识点,根据已知和所求的条件正确的构建出相关的全等三角形是解题的关键.

| A. | 16 | B. | 18 | C. | -18 | D. | 18或-18 |
| A. | x≠-1 | B. | x≠0 | C. | x≠1 | D. | x>1 |