题目内容
18.在△ABC中,BC=3,中线CD⊥BC,若BD-CD=1,求AB的长及sinB的值.分析 根据题意画出图形,设CD=x,BD=x+1,由勾股定理可得x,可得AB,利用直角三角形的边角关系可得sinB.
解答  解:如图,设CD=x,则BD=x+1,AB=2x+2,
解:如图,设CD=x,则BD=x+1,AB=2x+2,
∵CD⊥BC,
∴△BCD为直角三角形,
在Rt△BCD中,
由勾股定理得,BC2+CD2=BD2,
即9+x2=(x+1)2,
解得:x=4,
∴CD=4,BD=5,AB=10,
sinB=$\frac{CD}{BD}$=$\frac{4}{5}$.
点评 本题主要考查了勾股定理,解直角三角形,根据题意画出图形,掌握正弦的定义是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.与$\sqrt{6}$最接近的整数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
10.用线段a,b,c作为三角形的三边,下列哪种情况不构成直角三角形( )
| A. | a=5,b=12,c=13 | B. | a:b:C=1:2:$\sqrt{3}$ | C. | a=8,b=9,c=10 | D. | a=b=3,c=3$\sqrt{2}$ |
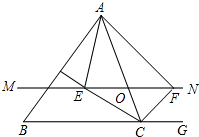 如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.