题目内容

8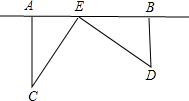．为了丰富少年儿童的业余生活，某社区要在如图中的AB所在的直线上建一图书室，本社区有两所学校所在的位置在点C和点D处，CA⊥AB于A，DB⊥AB于B．已知AB=2.5km，CA=1.5km，DB=1.0km，试问：图书室E应该建在距点A多少km处，才能使它到两所学校的距离相等？

分析 根据题意表示出AE，EB的长，进而利用勾股定理求出即可．

解答 解：由题意可得：设AE=xkm，则EB=（2.5-x）km，
∵AC2+AE2=EC2，BE2+DB2=ED2，EC=DE，
∴AC2+AE2=BE2+DB2，
∴1.52+x2=（2.5-x）2+12，
解得：x=1．
答：图书室E应该建在距点A1km处，才能使它到两所学校的距离相等．

点评 此题主要考查了勾股定理的应用，得出AC2+AE2=BE2+DB2是解题关键．

练习册系列答案
相关题目
18．如图1，扇形AOB中，∠AOB=120°，C为半径OA上一点，CD∥OB，交$\widehat{AB}$于D点．
（1）①在图2中画出以OA、OB为邻边的菱形AOBE，并说明E点的位置．（不要求写菱形AOBE的画法）
     ②如图1，当CD=6，AC=1时，求半径OB的长．
（2）如图3，若扇形的圆心角∠AOB改为105°，C仍为半径OA上一点（C点不与O，A两点重合），CD∥OB，交$\widehat{AB}$于D点，若使CD≤OB，在图3中，画图并说明D点的运动范围．
19．已知y=$\sqrt{2016-x}$+$\sqrt{x-2016}$-2015，求$\sqrt{x+y}$的值．
16．一个菱形水池，它的两条对角线长的差为2m，水池的边长都是5m，则这个菱形水池的面积为24m2．
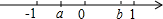3．表示实数a，b的点在数轴上的位置如图所示，化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$+|b-a|．
3．如图，平面直角坐标系xOy中，已知点A（2，3），线段AB垂直于y轴，垂足为B，将线段AB绕点A逆时针方向旋转90°，点B落在点C处，直线BC与x轴的交手点D．
（1）试求出点D的坐标；
（2）设直线AD交x轴于点H，y轴上有一动点P，点P从H点出发向B点运动，设线段PH长为t，过P点作MN∥x轴，交直线BC于M，交直线AD于N，若线段MN的长为y，试用含有t的代数式表示y；
（3）当y=$\frac{14}{3}$时，在y轴上是否存在一点F，使得以点A、P、F为顶点的三角形与△ACD相似？若存在，请求出此时F点的坐标；若不存在请说明理由．
（4）在坐标轴上是否存在点X，使直线XA与坐标轴夹角所得的正切值是2？若存在，请直接写出X的坐标．若不存在，请将题目条件中的2改为$\frac{1}{2}$，并直接写出X的坐标．
10．定义：如果两条线段将一个三角形分成3个等腰三角形，我们把这两条线段叫做这个三角形的三分线．
如图1，把一张顶角为36°的等腰三角形纸片剪两刀，分成3张小纸片，使每张小纸片都是等腰三角形，我们把这两条线段叫做等腰三角形的三分线．
（1）如图2，请用两种不同的方法画出顶角为45°的等腰三角形的三分线，并标注每个等腰三角形顶角的度数；（若两种方法分得的三角形成3对全等三角形，则视为同一种）
（2）如图3，△ABC中，AC=2，BC=3，∠C=2∠B，请画出△ABC的三分线，并求出三分线的长．
7．|-3|+2-1-20080．
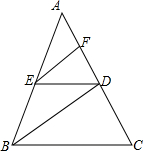8．如图，BD是∠ABC的平分线，ED∥BC，∠FED=∠BDE，
求证：EF是∠AED的平分线．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网