题目内容
13.正方形ABCD中,点P在射线BE上,∠APM=90°,CM平分∠DCE.(1)如图1,当P在BC上时,求证:∠MPC+∠E=45°;
(2)如图2,当P在BC的延长线上时,且BC=2PC,ME⊥BC的延长线于点E,探究四边形ABEM的面积与△APM的面积之间的数量关系,并证明你的结论.
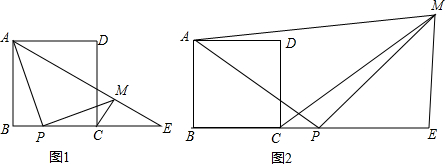
分析 (1)在BA上截取BP=BN,连接PN.只要证明△APN≌△PMC,即可推出PA=PM,可得△PAM是等腰直角三角形,推出∠AMP=∠MPE+∠E=45°;
(2)结论:$\frac{{S}_{△APM}}{{S}_{四边形ABEM}}$=$\frac{13}{25}$.设PC=a,首先证明△APB≌△PME,分别求出△APM,四边形ABEM的面积即可解决问题;
解答 (1)证明:在BA上截取BP=BN,连接PN.
∵四边形ABCD是正方形,
∴BA=BC,∠B=∠BCD=∠DCE=90°,
∵BN=BP,
∴AN=PC,∠BNP=45°,
∵CM平分∠DCE,
∴∠MCE=45°,
∴∠ANP=∠PCM=135°,
∵∠APM=90°,
∴∠APB+∠CPM=90°,
∵∠APB+∠BAO=90°,
∴∠PAN=∠CPM,
∴△APN≌△PMC,
∴PA=PM,
∴△PAM是等腰直角三角形,
∴∠AMP=∠MPE+∠E=45°,
即:∠MPC+∠E=45°;
(2)解:结论:$\frac{{S}_{△APM}}{{S}_{四边形ABEM}}$=$\frac{13}{25}$.
理由:如图2中,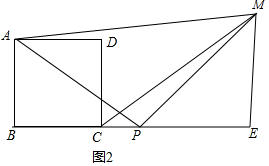
同法可证△APM是等腰直角三角形,
∴PA=PM,
∵∠APM=∠B=∠E=90°,
∴∠APB+∠MPE=90°,∠APB+∠BAP=90°,
∴∠PAB=∠MPE,
∴△APB≌△PME,设PC=a,则BC=2a,
在Rt△ABP中,PA2=(2a)2+(3a)2=13a2,
∴S△PAM=$\frac{1}{2}$PA2=$\frac{13}{2}$a2,
S四边形ABEM=2•$\frac{1}{2}$•3a•2a+$\frac{13}{2}$a2=$\frac{25}{2}$a2,
∴$\frac{{S}_{△APM}}{{S}_{四边形ABEM}}$=$\frac{\frac{13}{2}{a}^{2}}{\frac{25}{2}{a}^{2}}$=$\frac{13}{25}$.
点评 本题考查正方形的性质、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案 如图,已知∠A=∠D=90°,点E、F在线段BC上,DE与AF交于点O,且AB=DC,BE=CF.求证:
如图,已知∠A=∠D=90°,点E、F在线段BC上,DE与AF交于点O,且AB=DC,BE=CF.求证: 如图,为了测量山顶铁塔AE的高,小明在25m高的楼CD底部D测得塔顶A的仰角为45°,在楼顶C测得塔顶A的仰角36°52′.已知山高BE为58m,楼的底部D与山脚在同一水平线上,求该铁塔的高AE.(参考数据:sin36°52′≈0.60,tan36°52′≈0.75)
如图,为了测量山顶铁塔AE的高,小明在25m高的楼CD底部D测得塔顶A的仰角为45°,在楼顶C测得塔顶A的仰角36°52′.已知山高BE为58m,楼的底部D与山脚在同一水平线上,求该铁塔的高AE.(参考数据:sin36°52′≈0.60,tan36°52′≈0.75)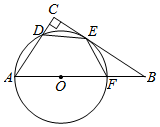 如图,在Rt△ABC中,∠C=90°,点D、E、F分别在AC、BC、AB边上,以AF为直径的⊙O恰好经过D、E,且DE=EF.
如图,在Rt△ABC中,∠C=90°,点D、E、F分别在AC、BC、AB边上,以AF为直径的⊙O恰好经过D、E,且DE=EF.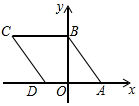 如图,四边形ABCD是菱形,A(3,0),B(0,4),则点C的坐标是(-5,4).
如图,四边形ABCD是菱形,A(3,0),B(0,4),则点C的坐标是(-5,4).