题目内容
4.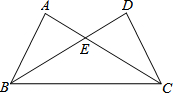 如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.
如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.(1)求证:△ABE≌△DCE;
(2)当∠AEB=56°时,求∠EBC的度数.
分析 (1)根据AAS推出两三角形全等即可;
(2)根据全等得出BE=CE,推出∠EBC=∠ECB,根据三角形外角性质求出即可.
解答 (1)证明:在△ABE和△DCE中,
$\left\{\begin{array}{l}{∠AEB=∠DEC}\\{∠A=∠D}\\{AB=CD}\end{array}\right.$,
∴△ABE≌△DCE(AAS);
(2)解:∵由(1)知,△ABE≌△DCE,
∴BE=CE,
∴∠EBC=∠ECB,
又∵∠AEB=∠EBC+∠ECB=56°,
∴∠EBC=28°.
点评 本题考查了全等三角形的性质和判定,三角形外角性质的应用,题目比较好,难度适中.

练习册系列答案
相关题目
9.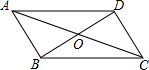 如图,在四边形ABCD中,对角线AC于BD相交于点O,下列条件中,不能判定四边形ABCD是平行四边形的是( )
如图,在四边形ABCD中,对角线AC于BD相交于点O,下列条件中,不能判定四边形ABCD是平行四边形的是( )
 如图,在四边形ABCD中,对角线AC于BD相交于点O,下列条件中,不能判定四边形ABCD是平行四边形的是( )
如图,在四边形ABCD中,对角线AC于BD相交于点O,下列条件中,不能判定四边形ABCD是平行四边形的是( )| A. | AB=CD,AD=BC | B. | AB∥CD,AD=BC | C. | AB∥CD,AD∥BC | D. | OA=OC,OB=OD |
10.下列说法中正确的是( )
| A. | 一个角的补角一定比这个角大 | B. | 一个角的补角一定是钝角 | ||
| C. | 一个直角的补角是直角 | D. | 一个锐角和一个钝角一定互为补角 |
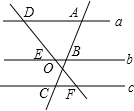 如图,直线a∥b,c∥b,AB=6,BC=3,则$\frac{DE}{DF}$=$\frac{2}{3}$.
如图,直线a∥b,c∥b,AB=6,BC=3,则$\frac{DE}{DF}$=$\frac{2}{3}$. 尺规作图,要求:保留作图痕迹,不写作法,不用说明理由.
尺规作图,要求:保留作图痕迹,不写作法,不用说明理由. 矩形ABCD的对角线AC、BD交于点O,∠AOD=120°,AC=4,则△ABO的周长为6.
矩形ABCD的对角线AC、BD交于点O,∠AOD=120°,AC=4,则△ABO的周长为6.