题目内容
6.若am=4,an=5,那么am-2n=$\frac{4}{25}$.分析 根据同底数幂的除法,底数不变指数相减;幂的乘方,底数不变指数相乘,即可解答.
解答 解:am-2n=${a}^{m}÷{a}^{2n}={a}^{m}÷({a}^{n})^{2}=4÷{5}^{2}=\frac{4}{25}$,
故答案为:$\frac{4}{25}$.
点评 本题考查同底数幂的除法,幂的乘方很容易混淆,一定要记准法则才能做题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.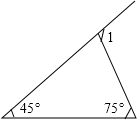 如图,∠1=( )度.
如图,∠1=( )度.
 如图,∠1=( )度.
如图,∠1=( )度.| A. | 110° | B. | 30° | C. | 60° | D. | 120° |
18.下列二次根式中的最简二次根式是( )
| A. | $\sqrt{9}$ | B. | $\sqrt{30}$ | C. | $\sqrt{18}$ | D. | $\sqrt{\frac{1}{3}}$ |
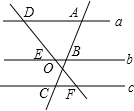 如图,直线a∥b,c∥b,AB=6,BC=3,则$\frac{DE}{DF}$=$\frac{2}{3}$.
如图,直线a∥b,c∥b,AB=6,BC=3,则$\frac{DE}{DF}$=$\frac{2}{3}$.