题目内容
 如图,一次函数y=kx+b(k≠0)与反比例函数y=
如图,一次函数y=kx+b(k≠0)与反比例函数y=| m |
| x |
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积;
(3)根据图象回答,在什么范围时,一次函数的值大于反比例函数的值.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)由一次函数y=kx+b(k≠0)与反比例函数y=
(m≠0)的图象有公共点A(1,2),D(a,-1),直接利用待定系数法求解即可求得答案;
(2)由直线l⊥x轴于点N(3,0),可求得点B与C的坐标,继而求得△ABC的面积;
(3)观察图象,即可求得在什么范围时,一次函数的值大于反比例函数的值.
| m |
| x |
(2)由直线l⊥x轴于点N(3,0),可求得点B与C的坐标,继而求得△ABC的面积;
(3)观察图象,即可求得在什么范围时,一次函数的值大于反比例函数的值.
解答:解:(1)∵一次函数y=kx+b(k≠0)与反比例函数y=
(m≠0)的图象有公共点A(1,2),D(a,-1).
∴将点A代入反比例函数y=
可得:2=
,
解得:m=2,
∴反比例函数的解析式为:y=
;
将D(a,-1)代入反比例函数的解析式y=
,得:-1=
,
解得:a=-2,
∴点D(-2,-1),
将点A与D代入一次函数解析式得:
,
解得:
,
∴一次函数的解析式为:y=x+1;
(2)∵点N(3,0),
∴B与C的横坐标为3,
∴点B的纵坐标为:y=3+1=4,
点C的纵坐标为:y=
,
∴点B(3,4),点C(3,
),
∴BC=4-
=
,
∴S△ABC=
×
×(3-1)=
;
(3)如图,当-2<x<0或x>1时,一次函数的值大于反比例函数的值.
| m |
| x |
∴将点A代入反比例函数y=
| m |
| x |
| m |
| 1 |
解得:m=2,
∴反比例函数的解析式为:y=
| 2 |
| x |
将D(a,-1)代入反比例函数的解析式y=
| 2 |
| x |
| 2 |
| a |
解得:a=-2,
∴点D(-2,-1),
将点A与D代入一次函数解析式得:
|
解得:
|
∴一次函数的解析式为:y=x+1;
(2)∵点N(3,0),
∴B与C的横坐标为3,
∴点B的纵坐标为:y=3+1=4,
点C的纵坐标为:y=
| 2 |
| 3 |
∴点B(3,4),点C(3,
| 2 |
| 3 |
∴BC=4-
| 2 |
| 3 |
| 10 |
| 3 |
∴S△ABC=
| 1 |
| 2 |
| 10 |
| 3 |
| 10 |
| 3 |
(3)如图,当-2<x<0或x>1时,一次函数的值大于反比例函数的值.
点评:此题考查了反比例函数与一次函数的交点问题.此题难度适中,注意掌握方程思想的应用是解此题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
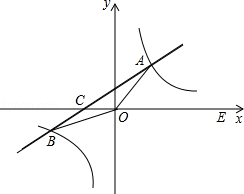 如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=的图象交于一、三象限内的A、B两点,直线AB与x轴交于点C,点B的坐标为(-6,n),线段OA=5,E为x轴正半轴上一点,且tan∠AOE=
如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=的图象交于一、三象限内的A、B两点,直线AB与x轴交于点C,点B的坐标为(-6,n),线段OA=5,E为x轴正半轴上一点,且tan∠AOE=
 “西气东输”是造福子孙后代的创世工程,现有两条高速公路l1、l2和两个城镇A、B(如图),准备建一个燃气控制中心站P,使中心站到两条公路距离相等,并且到两个城镇等距离,请你画出中心站的位置.(尺规作图,保留痕迹)
“西气东输”是造福子孙后代的创世工程,现有两条高速公路l1、l2和两个城镇A、B(如图),准备建一个燃气控制中心站P,使中心站到两条公路距离相等,并且到两个城镇等距离,请你画出中心站的位置.(尺规作图,保留痕迹)
 如图,反比例函数y=
如图,反比例函数y=