题目内容
1.计算下面两组算式:(1)(3×4)2与32×42,[(-$\frac{1}{3}$)×9]2与[(-$\frac{1}{3}$)]2×92,看一看每组两个算式的结果是否相等?
(2)想一想:(ab)2等于什么?a2b2
(3)猜一猜:当n为正整数,(ab)n等于什么?试证明你的结论.
分析 (1)先根据题中所给的式子得出规律即可;
(2)(3)根据(1)中的规律即可得出结论.
解答 解:(1)∵(3×4)2=122=144,32×42=9×16=144;
[(-$\frac{1}{3}$)×9]2=(-3)2=9,(-$\frac{1}{3}$)2×92=$\frac{1}{9}$×81=9,
∴每组两个算式的结论相同;
(2)由(1)可知,(ab)2=a2b2;
故答案为:a2b2.
(3)猜想,当n为正整数时,(ab)n=an•bn.
点评 本题考查的是有理数的乘方,根据题意找出规律是解答此题的关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
16.下列各项正确的个数为( )
①-(-2)2=4;②15=5;③(-1)2n=2n(n为自然数);④(-1)2n+1 =-1(n为自然数):⑤若x2>0,则x>0;⑥若x3<0,则x<0.
①-(-2)2=4;②15=5;③(-1)2n=2n(n为自然数);④(-1)2n+1 =-1(n为自然数):⑤若x2>0,则x>0;⑥若x3<0,则x<0.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
11.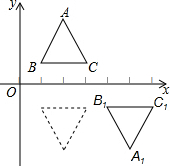 在平面直角坐标系中,把△ABC先沿x轴翻折,再向右平移3个单位得到△A1B1C1现把这两步操作规定为一种变换.如图,已知等边三角形ABC的顶点B、C的坐标分别是(1,1)、(3,1),把三角形经过连续5次这种变换得到三角形△A5B5C5,则点A的对应点A5的坐标是( )
在平面直角坐标系中,把△ABC先沿x轴翻折,再向右平移3个单位得到△A1B1C1现把这两步操作规定为一种变换.如图,已知等边三角形ABC的顶点B、C的坐标分别是(1,1)、(3,1),把三角形经过连续5次这种变换得到三角形△A5B5C5,则点A的对应点A5的坐标是( )
 在平面直角坐标系中,把△ABC先沿x轴翻折,再向右平移3个单位得到△A1B1C1现把这两步操作规定为一种变换.如图,已知等边三角形ABC的顶点B、C的坐标分别是(1,1)、(3,1),把三角形经过连续5次这种变换得到三角形△A5B5C5,则点A的对应点A5的坐标是( )
在平面直角坐标系中,把△ABC先沿x轴翻折,再向右平移3个单位得到△A1B1C1现把这两步操作规定为一种变换.如图,已知等边三角形ABC的顶点B、C的坐标分别是(1,1)、(3,1),把三角形经过连续5次这种变换得到三角形△A5B5C5,则点A的对应点A5的坐标是( )| A. | (5,-$\sqrt{3}$) | B. | (14,1+$\sqrt{3}$) | C. | (17,-1-$\sqrt{3}$) | D. | (20,1+$\sqrt{3}$) |
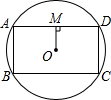 如图,矩形ABCD内接于⊙O,OM⊥AD,MO=3,AD=8.求:
如图,矩形ABCD内接于⊙O,OM⊥AD,MO=3,AD=8.求:
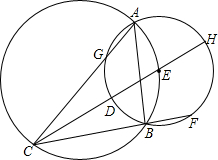 如图,⊙E的圆心在⊙O上,⊙E交⊙O于A、B两点,⊙O的弦CE所在直线交⊙E于点D、H,CB的延长线交⊙E于点F.
如图,⊙E的圆心在⊙O上,⊙E交⊙O于A、B两点,⊙O的弦CE所在直线交⊙E于点D、H,CB的延长线交⊙E于点F.