题目内容
17.已知:x=$\frac{1}{2+\sqrt{3}}$,y=$\frac{1}{2-\sqrt{3}}$,若x的整数部分是m,y的小数部分是n,求5m2+(x-n)2-y的值.分析 首先化简x=$\frac{1}{2+\sqrt{3}}$=2-$\sqrt{3}$,整数部分是m=0;y=$\frac{1}{2-\sqrt{3}}$=2+$\sqrt{3}$,小数部分是n=$\sqrt{3}$-1,由此进一步代入求得答案即可.
解答 解:∵x=$\frac{1}{2+\sqrt{3}}$=2-$\sqrt{3}$,y=$\frac{1}{2-\sqrt{3}}$=2+$\sqrt{3}$,
∴x的整数部分是m=0,y的小数部分是n=$\sqrt{3}$-1,
∴5m2+(x-n)2-y
=0+(3-2$\sqrt{3}$)2-(2+$\sqrt{3}$)
=21-12$\sqrt{3}$-2-$\sqrt{3}$
=19-13$\sqrt{3}$.
点评 此题考查二次根式的化简求值,无理数的估算,掌握化简的方法和计算的方法是解决问题的关键.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
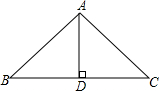 如图,在△ABC中,AB=AC,AD⊥BD于D.若AB=5,BD=4,求△ABC的周长.
如图,在△ABC中,AB=AC,AD⊥BD于D.若AB=5,BD=4,求△ABC的周长.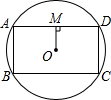 如图,矩形ABCD内接于⊙O,OM⊥AD,MO=3,AD=8.求:
如图,矩形ABCD内接于⊙O,OM⊥AD,MO=3,AD=8.求: