题目内容
12. 如图,将Rt△ABC沿BC边所在的直线向左平移6个单位,得到Rt△DEF,AB=8,DG=3,则四边形GCFD的面积为39.
如图,将Rt△ABC沿BC边所在的直线向左平移6个单位,得到Rt△DEF,AB=8,DG=3,则四边形GCFD的面积为39.
分析 根据平移的性质可得DE=AB,然后求出GE,再判断出四边形GCFD的面积等于四边形ABEG的面积,最后利用梯形的面积公式列式计算即可得解.
解答 解:∵将Rt△ABC沿射线BC方向平移得到△DEF,
∴DE=AB=8,
∵DG=3,
∴GE=DE-DG=5,
∵∠B=90°,
∴四边形ABEG是梯形,
S四边形GCFD=S△DEF-S△CEG=S△ABC-S△CEG=S梯形ABEG
=$\frac{1}{2}$(AB+GE)•BE
=$\frac{1}{2}$×(8+5)×6
=39.
故答案为:39.
点评 本题考查平移的基本性质:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等;本题判断出阴影部分的面积与四边形的面积相等是解题的关键.

练习册系列答案
相关题目
8.如图所示的正三棱柱,它的主视图、俯视图、左视图的顺序是( )


| A. | ①②③ | B. | ②①③ | C. | ③①② | D. | ①③② |
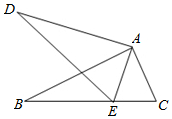 如图,在△ABC和△ADE中,点E在BC边上,∠B=∠D,AB=AD,∠BAD=∠CAE.
如图,在△ABC和△ADE中,点E在BC边上,∠B=∠D,AB=AD,∠BAD=∠CAE.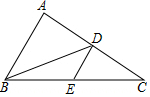 如图,在△ABC中,BD是边AC上的中线,E是BC的中点,连接DE.如果△BDE的面积为2,那么△ABC的面积为8.
如图,在△ABC中,BD是边AC上的中线,E是BC的中点,连接DE.如果△BDE的面积为2,那么△ABC的面积为8. 完成下列推理过程
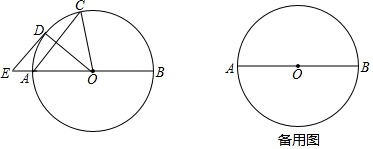
完成下列推理过程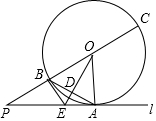 如图,直线l与⊙O相切于点A,点P在直线l上,直线PO交⊙O于点B,C,OD⊥AB,垂足为D,交PA于点E.
如图,直线l与⊙O相切于点A,点P在直线l上,直线PO交⊙O于点B,C,OD⊥AB,垂足为D,交PA于点E.