��Ŀ����
8��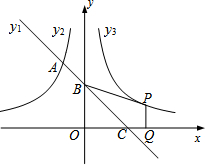 ��ͼ��һ�κ��� y1=kx+2��ͼ���뷴��������y2=-$\frac{3}{x}$��x��0����ͼ���ཻ��A�㣬��y�ᡢx��ֱ��ཻ��B��C���㣬��BC=2AB��
��ͼ��һ�κ��� y1=kx+2��ͼ���뷴��������y2=-$\frac{3}{x}$��x��0����ͼ���ཻ��A�㣬��y�ᡢx��ֱ��ཻ��B��C���㣬��BC=2AB����1����һ�κ����Ľ���ʽ����ֱ��д��ʹ��y1��y2��x��ȡֵ��Χ��
��2���躯��y3=$\frac{a}{x}$��x��0����ͼ����y2=-$\frac{3}{x}$��x��0����ͼ�����y��Գƣ���y3=$\frac{a}{x}$��x��0����ͼ����ȡһ��P��P��ĺ��������2������P��PQ��x�ᣬ����ΪQ�����ı���BCQP���������2����P������꣮
���� ��1����һ�κ�������y=0�����x=2�������B�����꣬��A��AH��x����H�������������A�����꣬����һ�κ�������ʽ�����k��ֵ�������һ�κ�������ʽ�����ͼ������y1��y2��x��ȡֵ��Χ��
��2���ɶԳ��Կ����y3=$\frac{a}{x}$�Ľ���ʽ����P������Ϊ��m��n��������OP�������ı���BCQP����������m��ֵ�������P�����꣮
��� �⣺��1����y1=kx+2�У���x=0�������y1=2��
��B��0��2����
��ͼ1����AH��x����H��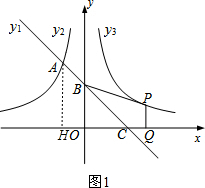
��BC=2AB��
��AC=$\frac{3}{2}$BC��
��AH=$\frac{3}{2}$OB=3��
��A��-1��3����
����y1=kx+2���ɵ�3=-k+2�����k=-1��
��һ�κ�������ʽΪy1=-x+2��
��A��������-1��3����
�൱-1��x��0ʱ��y1��y2��
��2����y3=$\frac{a}{x}$��x��0����ͼ����y2=-$\frac{3}{x}$��x��0����ͼ�����y��Գƣ�
��y3=$\frac{3}{x}$��x��0����
��P��m��n��������m��2����ͼ2������OP��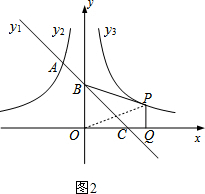
��S�ı���BOQP=S��BOP+S��POQ=S��BOC+S�ı���BCQP��
��$\frac{1}{2}$��2��m+$\frac{1}{2}$��3=$\frac{1}{2}$��2��2+2�����m=$\frac{5}{2}$��
��P��$\frac{5}{2}$��$\frac{6}{5}$����
���� ������Ҫ����һ�κ����뷴���������Ľ������⣬����������ͼ��Ľ�����������ÿ����������ʽ�ǽ���Ĺؼ���ע�����ν��˼���Ӧ�ã�

| A�� | 2��2 | B�� | -2��2 | C�� | -2��-2 | D�� | 2��-2 |
 ��ͼ������ƽ�ƣ�С���ϵĵ�A�Ƶ��˵�B��λ�ã��뻭��ƽ�ƺ��С����
��ͼ������ƽ�ƣ�С���ϵĵ�A�Ƶ��˵�B��λ�ã��뻭��ƽ�ƺ��С����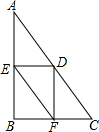 ��ͼ����ABC�У���B=90�㣬AB=8��BC=6����D��AC�ϵ�����һ�㣬����D��DE��AB�ڵ�E��DF��BC�ڵ�F������EF����EF����Сֵ��4.8��
��ͼ����ABC�У���B=90�㣬AB=8��BC=6����D��AC�ϵ�����һ�㣬����D��DE��AB�ڵ�E��DF��BC�ڵ�F������EF����EF����Сֵ��4.8��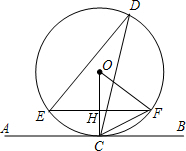 ��ͼ��ֱ��AB���O�����ڵ�C����EF��AB��OC��H��D�ǡ�O��һ�㣬����DE��DC��OF��
��ͼ��ֱ��AB���O�����ڵ�C����EF��AB��OC��H��D�ǡ�O��һ�㣬����DE��DC��OF�� 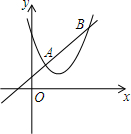 ��ͼ��ֱ��y=x+1��������y=x2-2mx+m2+m����A��B���㣨A��B��ߣ�����֤������mΪ��ֵ��AB�ij���Ϊ��ֵ��
��ͼ��ֱ��y=x+1��������y=x2-2mx+m2+m����A��B���㣨A��B��ߣ�����֤������mΪ��ֵ��AB�ij���Ϊ��ֵ��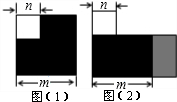 С��ͬѧ��ͼ��1���е���Ӱ���֣��߳�Ϊm�Ĵ�����������һ����Ϊn��С�����Σ�ƴ����һ�������Σ���ͼ2�����Ƚ�����ͼ��������Եó��Ľ�����m2-n2=��m+n����m-n�� ���ú�m��n��ʽ�ӱ��
С��ͬѧ��ͼ��1���е���Ӱ���֣��߳�Ϊm�Ĵ�����������һ����Ϊn��С�����Σ�ƴ����һ�������Σ���ͼ2�����Ƚ�����ͼ��������Եó��Ľ�����m2-n2=��m+n����m-n�� ���ú�m��n��ʽ�ӱ��