题目内容
20.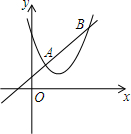 如图,直线y=x+1与抛物线y=x2-2mx+m2+m交于A、B两点(A在B左边).求证:无论m为何值,AB的长总为定值.
如图,直线y=x+1与抛物线y=x2-2mx+m2+m交于A、B两点(A在B左边).求证:无论m为何值,AB的长总为定值.
分析 联立方程求得A、B的坐标,然后根据勾股定理即可求得.
解答 解:∵直线y=x+1与抛物线y=x2-2mx+m2+m交于A、B两点,
∴$\left\{\begin{array}{l}{y=x+1}\\{y={x}^{2}-2mx+{m}^{2}+m}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=\frac{2m+1-\sqrt{5}}{2}}\\{y=\frac{2m+3-\sqrt{5}}{2}}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{2m+1+\sqrt{5}}{2}}\\{y=\frac{2m+3+\sqrt{5}}{2}}\end{array}\right.$
∴AB=$\sqrt{(\frac{2m+1+\sqrt{5}}{2}-\frac{2m+1-\sqrt{5}}{2})^{2}+(\frac{2m+3+\sqrt{5}}{2}{-\frac{2m+3-\sqrt{5}}{2})}^{2}}$=$\sqrt{10}$.
∴无论m为何值,AB的长总为定值$\sqrt{10}$.
点评 本题考查了二次函数的性质,求得直线和抛物线的交点是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.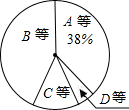 某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成下面的频数分布表和扇形统计图.
某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成下面的频数分布表和扇形统计图.
(1)试直接写出x=12,y=0.02;
(2)求C等的扇形的圆心角的度数;
(3)如果该校九年级共有男生200名,试估计这200名男生中成绩达到A等和B等的人数共有多少人?
 某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成下面的频数分布表和扇形统计图.
某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成下面的频数分布表和扇形统计图.| 等第 | 成绩(得分) | 频数(人数) | 频率 |
| A | 10分 | 7 | 0.14 |
| 9分 | x | ||
| B | 8分 | 15 | 0.30 |
| 7分 | 8 | 0.16 | |
| C | 6分 | 4 | 0.08 |
| 5分 | y | ||
| D | 5分以下 | 3 | 0.06 |
| 合计 | 50 | 1.00 |
(2)求C等的扇形的圆心角的度数;
(3)如果该校九年级共有男生200名,试估计这200名男生中成绩达到A等和B等的人数共有多少人?
9.验光师测的一组关于近视眼镜的度数y与镜片的焦距x的数据,如表:
则y关于x的函数关系式是y=$\frac{100}{x}$.
| y(单位:度) | 100 | 200 | 400 | 500 | … |
| x(单位:米) | 1.00 | 0.50 | 0.25 | 0.20 | … |
10. 如图,在△ABC中,∠BAC=90°,AD⊥BC于D,DC=4,BC=9,则AC为( )
如图,在△ABC中,∠BAC=90°,AD⊥BC于D,DC=4,BC=9,则AC为( )
 如图,在△ABC中,∠BAC=90°,AD⊥BC于D,DC=4,BC=9,则AC为( )
如图,在△ABC中,∠BAC=90°,AD⊥BC于D,DC=4,BC=9,则AC为( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
 如图,?ABCD的一边AB为直径的⊙O过点C,连结OC,若∠AOC=80°,则∠BCD=140度.
如图,?ABCD的一边AB为直径的⊙O过点C,连结OC,若∠AOC=80°,则∠BCD=140度.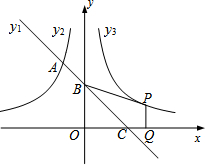 如图,一次函数 y1=kx+2的图象与反比例函数y2=-$\frac{3}{x}$(x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且BC=2AB.
如图,一次函数 y1=kx+2的图象与反比例函数y2=-$\frac{3}{x}$(x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且BC=2AB.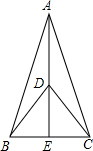 如图,在△ABC中,点E在BC上,点D在AE上,∠ABD=∠ACD,∠BDE=∠CDE.试说明BE=CE.
如图,在△ABC中,点E在BC上,点D在AE上,∠ABD=∠ACD,∠BDE=∠CDE.试说明BE=CE.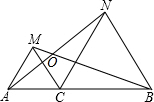 如图,点C为线段AB上一点,△ACM,△CBN是等边三角形,求证:AN=BM.
如图,点C为线段AB上一点,△ACM,△CBN是等边三角形,求证:AN=BM. 按图所示分割正方形,根据图中面积的不同表示方法写关于a、b的等式(a+b)2=a2+2ab+b2.
按图所示分割正方形,根据图中面积的不同表示方法写关于a、b的等式(a+b)2=a2+2ab+b2.