题目内容
17.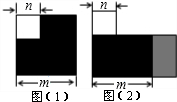 小明同学将图(1)中的阴影部分(边长为m的大正方形中有一个边为n的小正方形)拼成了一个长方形(如图2),比较两个图的面积可以得出的结论是m2-n2=(m+n)(m-n) (用含m,n的式子表达)
小明同学将图(1)中的阴影部分(边长为m的大正方形中有一个边为n的小正方形)拼成了一个长方形(如图2),比较两个图的面积可以得出的结论是m2-n2=(m+n)(m-n) (用含m,n的式子表达)运用所得公式,计算:
(1)20102-2009×2011
(2)(x-2y+1)(x+2y-1)
分析 根据题意分别求得(1)与(2)中阴影部分的面积,由两图形阴影面积相等,即可求得答案.
(1)利用平方差公式,即可解答;
(2)利用平方差公式,即可解答.
解答 解:根据题意得:
(1)中阴影部分的面积为:m2-n2;
(2)中阴影部分的面积为:(m+n)(m-n).
∵两图形阴影面积相等,
∴可以得到的结论是:m2-n2=(m-n)(m+n).
故答案为:m2-n2=(m-n)(m+n).
(1)20102-2009×2011
=20102-(2010-1)(2010+1)
=20102-20102+1
=1.
(2)(x-2y+1)(x+2y-1)
=[x-(2y-1)][x+(2y-1)]
=x2-(2y-1)2
=x2-4y2+4y-1.
点评 本题主要考查了平方差公式的几何表示,表示出图形阴影部分面积是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.点P与点Q(-3,2)关于原点对称,则点P的坐标是( )
| A. | (-3,2) | B. | (2,-3) | C. | (3,-2) | D. | (-2,3) |
9.验光师测的一组关于近视眼镜的度数y与镜片的焦距x的数据,如表:
则y关于x的函数关系式是y=$\frac{100}{x}$.
| y(单位:度) | 100 | 200 | 400 | 500 | … |
| x(单位:米) | 1.00 | 0.50 | 0.25 | 0.20 | … |
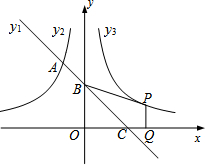 如图,一次函数 y1=kx+2的图象与反比例函数y2=-$\frac{3}{x}$(x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且BC=2AB.
如图,一次函数 y1=kx+2的图象与反比例函数y2=-$\frac{3}{x}$(x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且BC=2AB.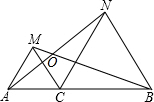 如图,点C为线段AB上一点,△ACM,△CBN是等边三角形,求证:AN=BM.
如图,点C为线段AB上一点,△ACM,△CBN是等边三角形,求证:AN=BM. 按图所示分割正方形,根据图中面积的不同表示方法写关于a、b的等式(a+b)2=a2+2ab+b2.
按图所示分割正方形,根据图中面积的不同表示方法写关于a、b的等式(a+b)2=a2+2ab+b2.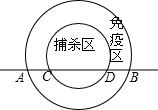 高致病性禽流感是比SARS传染速度更快的传染病,为了防止禽流感蔓延,政府规定离疫点3km范围内为扑杀区;离疫点3km-5km范围内为免疫区,对扑杀区与免疫区内的村庄、道路实行全封闭管理.现有一条笔直的公路AB通过禽流感病区,如图,在扑杀区内公路CD长为4km.
高致病性禽流感是比SARS传染速度更快的传染病,为了防止禽流感蔓延,政府规定离疫点3km范围内为扑杀区;离疫点3km-5km范围内为免疫区,对扑杀区与免疫区内的村庄、道路实行全封闭管理.现有一条笔直的公路AB通过禽流感病区,如图,在扑杀区内公路CD长为4km. (1)如图,若∠1=∠2,则AB∥CD,试判断命题的真假:假(填“真”或“假”).
(1)如图,若∠1=∠2,则AB∥CD,试判断命题的真假:假(填“真”或“假”).