题目内容
3.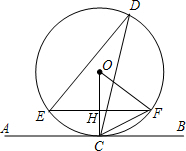 如图,直线AB与⊙O相切于点C,弦EF∥AB交OC于H,D是⊙O上一点,连结DE、DC、OF.
如图,直线AB与⊙O相切于点C,弦EF∥AB交OC于H,D是⊙O上一点,连结DE、DC、OF. (1)若∠EDC=30°,则∠COF=60度;
(2)若EF=8,CH=2,求⊙O的半径.
分析 (1)根据切线的性质可知,OC⊥AB,由于EF∥AB,故OC⊥EF,由垂径定理可知$\widehat{EC}=\widehat{CF}$,根据同圆或等圆中同弧或等弧所对的圆周角等于圆心角的一半解答即可.
(2)设⊙O的半径为r,根据直角三角形的性质及勾股定理列出方程解答即可.
解答 解:(1)∵直线AB与⊙O相切于点C,
∴OC⊥AB;
∵EF∥AB,
∴OC⊥EF,
∴$\widehat{EC}=\widehat{CF}$,
∴∠COF=2∠EDC=2×30°=60°,
故答案为:60;
(2)设⊙O的半径为r,则OH=OC-CH=r-2,
∵EF=8,OH⊥EF,
∴HF=$\frac{1}{2}$EF=4,
在Rt△OHF中,
由勾股定理得:OF2=OH2+HF2,即r2=(r-2)2+42,
解得:r=5,
∴⊙O的半径是5.
点评 本题考查了切线的性质,圆周角定理以及勾股定理的运用,综合性比较强,熟练掌握切线的性质定理是解题的关键.

练习册系列答案
相关题目
11.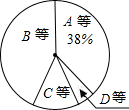 某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成下面的频数分布表和扇形统计图.
某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成下面的频数分布表和扇形统计图.
(1)试直接写出x=12,y=0.02;
(2)求C等的扇形的圆心角的度数;
(3)如果该校九年级共有男生200名,试估计这200名男生中成绩达到A等和B等的人数共有多少人?
 某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成下面的频数分布表和扇形统计图.
某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成下面的频数分布表和扇形统计图.| 等第 | 成绩(得分) | 频数(人数) | 频率 |
| A | 10分 | 7 | 0.14 |
| 9分 | x | ||
| B | 8分 | 15 | 0.30 |
| 7分 | 8 | 0.16 | |
| C | 6分 | 4 | 0.08 |
| 5分 | y | ||
| D | 5分以下 | 3 | 0.06 |
| 合计 | 50 | 1.00 |
(2)求C等的扇形的圆心角的度数;
(3)如果该校九年级共有男生200名,试估计这200名男生中成绩达到A等和B等的人数共有多少人?
13.若等腰三角形的一个角为70°,则顶角为( )
| A. | 70° | B. | 40° | C. | 40°或70° | D. | 80° |
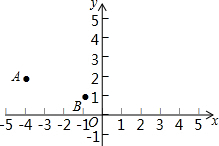 如图,A(-4,2),B(-1,1),在x轴上找一点P,使|PA-PB|的值最大,求点P的坐标.
如图,A(-4,2),B(-1,1),在x轴上找一点P,使|PA-PB|的值最大,求点P的坐标.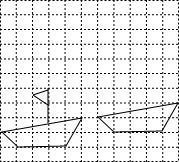 (1)如图,网格内每个小正方形的边长为1,小船从左边移到右边新的位置,试分析小船是怎样移到新的位置的,并将小船运动中缺少的部分补上.
(1)如图,网格内每个小正方形的边长为1,小船从左边移到右边新的位置,试分析小船是怎样移到新的位置的,并将小船运动中缺少的部分补上.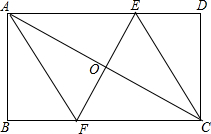 如图,在矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD,BC于点E,F,垂足为点O.
如图,在矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD,BC于点E,F,垂足为点O.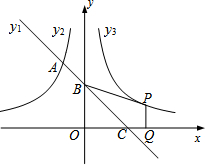 如图,一次函数 y1=kx+2的图象与反比例函数y2=-$\frac{3}{x}$(x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且BC=2AB.
如图,一次函数 y1=kx+2的图象与反比例函数y2=-$\frac{3}{x}$(x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且BC=2AB.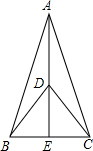 如图,在△ABC中,点E在BC上,点D在AE上,∠ABD=∠ACD,∠BDE=∠CDE.试说明BE=CE.
如图,在△ABC中,点E在BC上,点D在AE上,∠ABD=∠ACD,∠BDE=∠CDE.试说明BE=CE. 按图所示分割正方形,根据图中面积的不同表示方法写关于a、b的等式(a+b)2=a2+2ab+b2.
按图所示分割正方形,根据图中面积的不同表示方法写关于a、b的等式(a+b)2=a2+2ab+b2.