题目内容
3.抛物线y=x2+2x+c与y轴相交于点C,点O为坐标原点,点A是抛物线y=x2+2x+c与x轴的公共点,若OA=OC,则点A的坐标为(-3,0)、(1,0).分析 由OA=OC=|c|及点A是抛物线与x轴的公共点可得点A的坐标为(c,0)或(-c,0),将点A坐标代入抛物线解析式可求得c的值.
解答 解:根据题意,知:OA=OC=|c|,
∵点A是抛物线y=x2+2x+c与x轴的公共点,
∴点A的坐标为(c,0)或(-c,0),
将点A(c,0)代入y=x2+2x+c得:c2+2c+c=0,
解得:c=0(舍)或c=-3,
则点A的坐标为(-3,0);
将点A(-c,0)代入y=x2+2x+c,得:(-c)2-2c+c=0,即c2-c=0,
解得:c=0(舍)或c=1,
则点A的坐标为(1,0);
故答案为:(-3,0)、(1,0).
点评 本题主要考查抛物线与x轴的交点,结合题意表示出点A的坐标是解题的前提,由抛物线个与x轴的交点求得c值是解题的关键.

练习册系列答案
相关题目
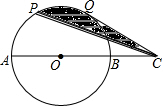 如图,P,Q是半圆O的三等分点,C是直径AB延长线上的一点,若AB=6cm,求阴影部分的面积.
如图,P,Q是半圆O的三等分点,C是直径AB延长线上的一点,若AB=6cm,求阴影部分的面积.