题目内容
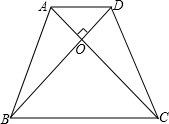 如图,在等腰梯形ABCD中,AD∥BC,AC、BD为对角线,且AC⊥BD,AD=3,BC=7,则梯形的对角线为
如图,在等腰梯形ABCD中,AD∥BC,AC、BD为对角线,且AC⊥BD,AD=3,BC=7,则梯形的对角线为考点:等腰梯形的性质
专题:
分析:过点D作DE∥AC交BC的延长线于点E,作DF⊥BC于F,证平行四边形ADEC,推出AC=DE=BD,∠BDE=90°,根据等腰三角形性质推出BF=DF=EF=
BE,求出DF、DE,根据梯形的面积公式求出即可.
| 1 |
| 2 |
解答:解:过点D作DE∥AC交BC的延长线于点E,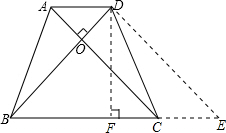
∵AD∥BC,
即AD∥CE,
∴四边形ACED是平行四边形,
∴AD=CE=3,AC=DE,
在等腰梯形ABCD中,AC=DB,
∴DB=DE,
∵AC⊥BD,AC∥DE,
∴∠EDB=∠BOC=90°,
∴DB⊥DE,
∴△BDE是等腰直角三角形,
作DF⊥BC于F,
∴BF=EF,
∴DF=
BE=5,
则DE=AC=5
,
∴S梯形ABCD=
(AD+BC)•DF=
(3+7)×5=25,
故答案为:5
,25.

∵AD∥BC,
即AD∥CE,
∴四边形ACED是平行四边形,
∴AD=CE=3,AC=DE,
在等腰梯形ABCD中,AC=DB,
∴DB=DE,
∵AC⊥BD,AC∥DE,
∴∠EDB=∠BOC=90°,
∴DB⊥DE,
∴△BDE是等腰直角三角形,
作DF⊥BC于F,
∴BF=EF,
∴DF=
| 1 |
| 2 |
则DE=AC=5
| 2 |
∴S梯形ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:5
| 2 |
点评:本题主要考查对等腰三角形性质,平行四边形的性质和判定,等腰梯形的性质,等腰直角三角形等知识点的理解和掌握,能求出高DF的长是解此题的关键.

练习册系列答案
相关题目
 如图,三角形ABC中,根据下列语句画出图形.
如图,三角形ABC中,根据下列语句画出图形. 如图,∠A=∠D=90°,AC=BD,
如图,∠A=∠D=90°,AC=BD, 如图,在△ABC中D,E是BC的三等分点,且△ADE是等边三角形,则∠BAC=
如图,在△ABC中D,E是BC的三等分点,且△ADE是等边三角形,则∠BAC= 如图,在正方形ABCD内作一个等边三角形ABE,连接DE,CE,有如下结论:
如图,在正方形ABCD内作一个等边三角形ABE,连接DE,CE,有如下结论: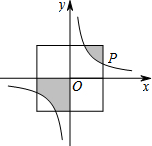 如图,在平面直角坐标系中,正方形的中心在原点O,且正方形的一组对边与x轴平行,点P(2a,a)是反比例函数y=
如图,在平面直角坐标系中,正方形的中心在原点O,且正方形的一组对边与x轴平行,点P(2a,a)是反比例函数y= 已知:如图,⊙O是△ABC的外接圆,AD为⊙O的直径,若AC=2,∠ABC=30°,则AD的长为
已知:如图,⊙O是△ABC的外接圆,AD为⊙O的直径,若AC=2,∠ABC=30°,则AD的长为