题目内容
 如图,∠A=∠D=90°,AC=BD,
如图,∠A=∠D=90°,AC=BD,(1)求证:AB=CD;
(2)请判断△OBC的形状,并说明理由.
考点:全等三角形的判定与性质
专题:
分析:(1)首先利用HL定理证明Rt△ABC≌Rt△DCB,则全等三角形的对应边相等,即AB=CD;
(2)△OBC是等腰三角形.根据(1)中全等三角形的性质可得∠OBC=∠OCB,再根据等角对等边可得BO=CO.
(2)△OBC是等腰三角形.根据(1)中全等三角形的性质可得∠OBC=∠OCB,再根据等角对等边可得BO=CO.
解答:(1)证明:在Rt△ABC和Rt△DCB中
,
∴Rt△ABC≌Rt△DCB(HL),
∴AB=CD;
(2)△OBC是等腰三角形.理由如下:
∵由(1)知,Rt△ABC≌Rt△DCB
∴∠OBC=∠OCB,
∴OB=OC.
|
∴Rt△ABC≌Rt△DCB(HL),
∴AB=CD;
(2)△OBC是等腰三角形.理由如下:
∵由(1)知,Rt△ABC≌Rt△DCB
∴∠OBC=∠OCB,
∴OB=OC.
点评:此题主要考查了全等三角形的判定,全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.

练习册系列答案
相关题目
 如图,在△ABC中,BC=AC,且CD∥AB,设△ABC的外心为O.
如图,在△ABC中,BC=AC,且CD∥AB,设△ABC的外心为O. 如图,网格图中的每一格的边长为1个单位长度,在网格中有A,B,C三个点,按要求完成下列各小题.
如图,网格图中的每一格的边长为1个单位长度,在网格中有A,B,C三个点,按要求完成下列各小题.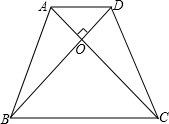 如图,在等腰梯形ABCD中,AD∥BC,AC、BD为对角线,且AC⊥BD,AD=3,BC=7,则梯形的对角线为
如图,在等腰梯形ABCD中,AD∥BC,AC、BD为对角线,且AC⊥BD,AD=3,BC=7,则梯形的对角线为