题目内容
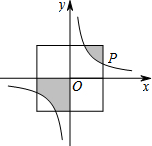 如图,在平面直角坐标系中,正方形的中心在原点O,且正方形的一组对边与x轴平行,点P(2a,a)是反比例函数y=
如图,在平面直角坐标系中,正方形的中心在原点O,且正方形的一组对边与x轴平行,点P(2a,a)是反比例函数y=| 2 |
| x |
考点:反比例函数图象的对称性
专题:计算题
分析:先利用反比例函数解析式y=
确定P点坐标为(2,1),由于正方形的中心在原点O,则正方形的面积为16,然后根据反比例函数图象关于原点中心对称得到阴影部分的面积为正方形面积的
.
| 2 |
| x |
| 1 |
| 4 |
解答:解:把P(2a,a)代入y=
得2a•a=2,解得a=1或-1,
∵点P在第一象限,
∴a=1,
∴P点坐标为(2,1),
∴正方形的面积=4×4=16,
∴图中阴影部分的面积=
S正方形=4.
故答案为4.
| 2 |
| x |
∵点P在第一象限,
∴a=1,
∴P点坐标为(2,1),
∴正方形的面积=4×4=16,
∴图中阴影部分的面积=
| 1 |
| 4 |
故答案为4.
点评:本题考查了反比例函数图象的对称性:反比例函数图象既是轴对称图形又是中心对称图形,对称轴分别是:①二、四象限的角平分线y=-x;②一、三象限的角平分线y=x;对称中心是:坐标原点.

练习册系列答案
相关题目
 一次越野赛跑中,当李明跑了1600米时,小刚跑了1450米,此后两人匀速跑的路程S(米)与时间t(秒)的关系如图,结合图象解答下列问题:(1)请你根据图象写出二条信息;
一次越野赛跑中,当李明跑了1600米时,小刚跑了1450米,此后两人匀速跑的路程S(米)与时间t(秒)的关系如图,结合图象解答下列问题:(1)请你根据图象写出二条信息;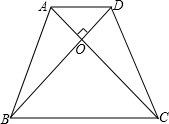 如图,在等腰梯形ABCD中,AD∥BC,AC、BD为对角线,且AC⊥BD,AD=3,BC=7,则梯形的对角线为
如图,在等腰梯形ABCD中,AD∥BC,AC、BD为对角线,且AC⊥BD,AD=3,BC=7,则梯形的对角线为 如图,过正方形ABCD的顶点B作直线l,过点A,C作l的垂线,垂足分别为点E,F.若AE=2,CF=6,则AB的长度为
如图,过正方形ABCD的顶点B作直线l,过点A,C作l的垂线,垂足分别为点E,F.若AE=2,CF=6,则AB的长度为 如图,点B在数轴上表示的数是-3,过B作AB垂直数轴,AB=2,以原点O为圆心,以AO长为半径在数轴的负半轴上截得OC=OA,那么C点在数轴上所表示的数是
如图,点B在数轴上表示的数是-3,过B作AB垂直数轴,AB=2,以原点O为圆心,以AO长为半径在数轴的负半轴上截得OC=OA,那么C点在数轴上所表示的数是