题目内容
已知：如图，⊙O是△ABC的外接圆，AD为⊙O的直径，若AC=2，∠ABC=30°，则AD的长为考点：圆周角定理,含30度角的直角三角形
专题：
分析：连接CD，则可得∠ADC=30°，在Rt△ADC中可求出AD的长．
解答：
解：连接CD．
∵AD为⊙O的直径，
∴∠ACD=90°．
则∠ADC=∠ABC=30°（圆周角定理），
在Rt△ADC中，∵∠ADC=30°，∠ACD=90°，
∴AD=2AC=4．
故答案为：4．
解：连接CD．∵AD为⊙O的直径，
∴∠ACD=90°．
则∠ADC=∠ABC=30°（圆周角定理），
在Rt△ADC中，∵∠ADC=30°，∠ACD=90°，
∴AD=2AC=4．
故答案为：4．
点评：本题考查了圆周角定理的知识，属于基础题，解答本题的关键是掌握圆周角定理的内容．
练习册系列答案
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
阳光课堂同步练习系列答案
相关题目
如图，在△ABC中，BC=AC，且CD∥AB，设△ABC的外心为O．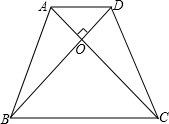
如图，在等腰梯形ABCD中，AD∥BC，AC、BD为对角线，且AC⊥BD，AD=3，BC=7，则梯形的对角线为