题目内容
如图，在△ABC中D，E是BC的三等分点，且△ADE是等边三角形，则∠BAC=考点：等边三角形的性质
专题：
分析：利用等边三角形的性质以及等腰三角形的性质得出∠B=∠BAD=∠C=∠EAC=30°，进而利用三角形内角和定理求出即可．
解答：解：∵E是BC的三等分点，且△ADE是等边三角形，
∴BD=DE=EC=AD=AE，∠ADE=∠AED=60°，
∴∠B=∠BAD=∠C=∠EAC=30°，
∴∠BAC=180°-∠B-∠C=120°．
故答案为：120°．
∴BD=DE=EC=AD=AE，∠ADE=∠AED=60°，
∴∠B=∠BAD=∠C=∠EAC=30°，
∴∠BAC=180°-∠B-∠C=120°．
故答案为：120°．
点评：此题主要考查了等边三角形的性质与等腰三角形的性质等知识，得出∠B=∠C的度数是解题关键．
练习册系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
某中学对全校学生1分钟跳绳的次数进行了统计，全校1分钟跳绳的平均次数是100次．某班体育委员统计了全班50名学生1分钟跳绳的成绩，列出的频数分布直方图如下（每个分组包括左端点，不包括右端点）．
如图，网格图中的每一格的边长为1个单位长度，在网格中有A，B，C三个点，按要求完成下列各小题．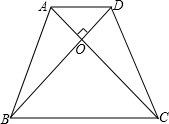
如图，在等腰梯形ABCD中，AD∥BC，AC、BD为对角线，且AC⊥BD，AD=3，BC=7，则梯形的对角线为
如图，把一块含有30°角的直角三角板两个顶点放在一把直尺的对边上，如果∠1=25°，那么∠2的度数为